Nächste Seite: 3.3 Prädikatsvervollständigung Vorige Seite: 3.1 Inferenz und Nichtmonotonie

3.2 Annahme der Weltabgeschlossenheit

Beginnen wir mit der (logisch) einfachen Welt einer Datenbank. Als Beispiel betrachten wir das folgende Fragment eines Fahrplans der Bundesbahn.

Wie wir bereits wissen, handelt es sich logisch hier um drei Fakten in der Form von Grundatomen. Die Theorie dieser drei Fakten besteht aus diesen selbst (und allen Tautologien sowie daraus gebildeten logischen Zusammensetzungen). Von einem Fahrplan bzw. einer entsprechenden Datenbank wird aber mehr erwartet. Fragt nämlich ein Kunde, ob es um einen Zug nach Buxtehude gibt, so wird bei diesem Sachverhalt die Antwort ``nein'', dh. logisch die Ableitung von erwartet. ``Stillschweigend'' oder ``vereinbarungsgemäß'' interpretieren wir einen solchen Fahrplan (und andere Datenbanken) so, daß in gewissem Umfang Aussagen, die nicht explizit genannt sind, als nichtgeltend zusätzlich angenommen werden. Die Annahme der Weltabgeschlossenheit (engl. closed world assumption) [Rei77] , kurz AWA, präzisiert diesen Umfang in der folgenden Weise.

Sei eine Menge von Formeln der Prädikatenlogik erster Stufe über einem Alphabet . Die unter der Annahme der Weltabgeschlossenheit erhaltene Theorie ist definiert durch

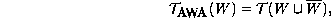
wobei

Wenn , wie in unserem Beispiel, nur aus Grundatomen besteht, dann besteht also aus allen bildbaren negierten Fakten, die unnegiert nicht in der Datenbank stehen. Nun ist es also möglich, auch logisch abzuleiten. Diese Lösung ist in Abbildung 3.1 veranschaulicht. Zwar behalten wir den klassischen Theorie- und Ableitungsbegriff bei, aber zu der Menge der gegebenen Aussagen wird eine davon abhängige Menge von Annahmen (wie die eben beschriebene negierte Faktenmenge) vereinbarungsgemäß hinzugenommen, bevor der Ableitungsmechanismus in Gang gesetzt wird.

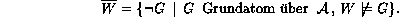
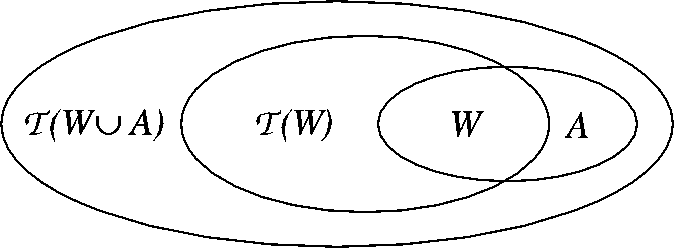
Abbildung 3.1: Die Hinzunahme von Annahmen

Eine Theorie heißt vollständig , wenn für jedes Grundatom über der gegebenen Sprache entweder oder gilt. Die Annahme der Weltabgeschlossenheit macht jede Datenbanktheorie zu einer vollständigen Theorie. Sie führt insgesamt zu einem nichtmonotonen Verhalten, denn die Hinzunahme eines weiteren Atoms erfordert die Entfernung einer impliziten Annahme, die dann nicht mehr zur Theorie gehört.

Wir haben schon in Abschnitt 3.1 erwähnt, daß die Inferenzrelation selbst als Wissen aufgefaßt werden kann. Genauer würde man hier von Meta-Wissen sprechen. Bei gegebenem (und ) ist die Menge der durch die AWA gemachten Annahmen eindeutig bestimmt, und zwar durch Wissen, das man ebenfalls der Meta-Ebene zuordnen würde. Es ist daher nicht überraschend, daß man die AWA nicht nur durch die bislang besprochene Erweiterung der Weltbeschreibung durch zusätzliche Annahmen, sondern äquivalent auch durch eine Modifikation von beschreiben kann.

Für beliebige Formeln , Grundatome und für jede beliebige Menge von Formeln der Prädikatenlogik erster Stufe über einem Alphabet sei die Relation induktiv wie folgt definiert.

1. Gilt , so auch .
2. Gilt , so gelte .
3. Gilt und , so auch .

Dann nennen wir

die unter der AWA erhaltene Theorie.

Nur die zweite dieser drei Regeln zur Definition von geht über das hinaus, was für die Tarskische Semantik gilt. In ihr wird offensichtlich genau die durch die AWA getroffene Maßgabe beschrieben. Offensichtlich gilt daher

In einem entsprechenden Kalkül für die Prädikatenlogik ergibt sich eine zusätzliche Kalkülregel, die der zweiten Regel entspricht und von der folgenden Gestalt ist.

Kalkülregeln dieser Gestalt werden uns in Abschnitt 3.7 im Zusammenhang mit der Reiterschen Ermangelungslogik in verallgemeinerter Form wieder begegnen.

Die AWA ist zwar einfach und scheint in einfachen Fällen genau den gewünschten Effekt zu haben. Leider löst sie das Phänomen des nichtmonotonen Schließens nicht in der gewünschten umfassenden Weise. Zunächst erkennen wir, daß wegen der Unentscheidbarkeit der Prädikatenlogik die Anwendbarkeit der oben gezeigten zweiten Regel unentscheidbar ist. Es ergibt sich also ein Problem im Hinblick auf ein mögliches Berechnungsverfahren; jedoch stoßen wir bei allen Ansätzen zur Nichtmonotonie auf Probleme von dieser Natur, durch die Grenzen der Berechenbarkeit sichtbar werden; sie besagen uns, daß wir nur innerhalb solcher Grenzen auf Erfolg hoffen können. Weiter ist die AWA von der Wahl der Prädikatsbezeichnungen abhängig; benennt man zB. ein Prädikat zu um, so ergibt sich offensichtlich ein anderes Verhalten der AWA. Darüber hinaus ergeben sich bei der AWA die durch die folgenden beiden Beispiele illustrierten Konsistenzprobleme.

Angenommen, unsere Welt sei allein durch die Formel beschrieben. Dann läßt sich hieraus klassisch weder noch folgern. Also besteht aus den Literalen . Die so entstehende Theorie ist nun offensichtlich widersprüchlich, während die ursprüngliche Welt konsistent ist. Die AWA kann also ausgehend von konsistenten Formelmengen zu inkonsistenten Theorien führen. Ein Verfahren, das Widersprüche generiert, die vorher nicht vorhanden waren, kann nicht als tauglich angesehen werden.

Auch in diesem Beispiel, das nur eine Variante des vorangegangenen Beispiels darstellt, führt die AWA zu einem Widerspruch. ergibt sich nämlich zu

Dann aber wird die Regel des Beispiels anwendbar und Liebt_Eiscreme(Larissa) also ableitbar, so daß der Widerspruch offensichtlich ist.

Man beachte in diesem Beispiel, das wir oft auch kurz als formulieren werden, die hier mit einem Abnormalitätsprädikat realisierte Technik, Regeln mit Ausnahmen logisch korrekt darzustellen, die wir in diesem und den nächsten beiden Abschnitten immer einsetzen werden. Natürlichsprachlich sind solche Regeln dadurch charakterisiert, daß sie in der Form ``normalerweise lieben Kinder Eiscreme'' formuliert (oder zumindest gedacht) werden. Semantisch läßt sich eine solche Regel wie in Abbildung 3.2 dargestellt illustrieren.

Abbildung 3.2: Die Interpretation einer Regel mit Ausnahmen

Die meisten Elemente der Extension von , also der Kinder, liegen in der Extension von , lieben also Eiscreme. Nur ein kleiner Teil der Kinder ist abnormal, auf den also die Regel nicht zutrifft.

Nach den enttäuschenden Einsichten, die sich aus diesen beiden Beispielen ergeben, stellt sich die Frage, ob es vielleicht Teilklassen von Formeln gibt, bei denen sich durch die AWA keine derartigen Widersprüche einschleichen. Eine solche Teilklasse werden wir nun angeben. Dies erfordert einige Vorbereitungen, wobei wir den Modellbegriff der Prädikatenlogik entsprechend unserer generellen Verabredung in Abschnitt 1.6 als bekannt voraussetzen.

Seien eine Formelmenge der Prädikatenlogik erster Stufe und sowie Modelle von . Dann ist ein Untermodell von bezüglich des Prädikats , geschrieben , genau dann, wenn die folgenden Bedingungen erfüllt sind:

1. D = D',
2. ,
3. und stimmen im übrigen überein.

heißt ein Untermodell von bezüglich einer Menge von im zugrundegelegten Alphabet enthaltenen Prädikatszeichen, , wenn die Bedingung (2) für alle gilt.
Besteht aus allen im Alphabet enthaltenen Prädikatszeichen oder ist die Prädikatsmenge eindeutig aus dem Kontext klar, so schreiben wir auch kurz .
Ein Modell einer Formelmenge wird als minimal bezeichnet genau dann, wenn für alle Modelle von gilt

Ein Modell einer Formelmenge wird als das kleinste Modell von bezeichnet genau dann, wenn für alle Modelle von mit gilt

Die letzten beiden Begriffe sind für Teilmengen der Prädikatszeichen entsprechend definiert.

In den meisten Anwendungsfällen lassen sich prädikatenlogische Formeln ohne wesentliche Einschränkung der Allgemeinheit auf Klauselform bringen. Klauselmengen haben die besonders angenehme Eigenschaft, daß eine Klauselmenge genau dann ein Modell hat, wenn sie ein Herbrandmodell hat. Ein Herbrandmodell ist dabei bekanntlich über den Zeichen des Alphabets der zugrundeliegenden Sprache gebildet. Es wird als eine Menge von Grundatomformeln repräsentiert. Dadurch reduziert sich die in der voranstehenden Definition eingeführte Untermodellbeziehung auf die Teilmengenbeziehung zwischen zwei Grundatomformelmengen. Für die nachfolgende Aussage 3.2 müssen wir uns auf diesen Fall von Herbrandmodellen beschränken (da er im allgemeinen nicht gilt).

Betrachtet man eine Formelmenge unter der AWA, so eliminiert man damit eine große Anzahl von Modellen -- nämlich all jene Modelle, die Grundatome aus der Menge der negierten nichtfolgerbaren Grundatome erfüllen. Tatsächlich besitzt eine konsistente Formelmenge unter der AWA dann nur noch ein einziges Herbrandmodell. Wenn die Formelmenge ein kleinstes Herbrandmodell besitzt, so kann man allgemein beweisen, daß dieses auch das einzige Herbrandmodell unter der AWA ist, was wir im folgenden Satz festhalten.

Ist eine konsistente Formelmenge, so ist konsistent genau dann, wenn ein kleinstes Herbrandmodell hat.

Eine syntaktische Variante dieses Satzes ist die folgende Aussage [GN89].

Ist eine konsistente Formelmenge, so ist konsistent genau dann, wenn es für jede Disjunktion von Grundatomen mit mindestens ein mit gibt, .

Hornformeln zeichnen sich genau durch die Eigenschaft aus, immer ein kleinstes Herbrandmodell zu haben [Llo84]. Somit ergibt sich aus dem vorletzten Satz das erstmals in [Rei77] erzielte Ergebnis.

Ist eine konsistente Menge von Hornformeln, so ist konsistent.

In der Tat sind die beiden Beispiele oben, die zu Widersprüchen geführt haben, eben keine Hornformeln, ebensowenig wie sie die Aussage des vorangegangenen Satzes erfüllen. Auch haben sie kein kleinstes Modell. So hat zB. zwei verschiedene minimale Modelle; im einen besteht die Interpretation von genau aus der von , im anderen aus der von , also sind beide Einermengen disjunkt.

Wir stehen natürlich nun immer noch vor der Frage, wie Nicht-Hornformeln hinsichtlich der AWA zu behandeln sind. Eine Möglichkeit, auch in diesem Fall Inkonsistenzen zu vermeiden, besteht in einer Anwendung der AWA nur auf eine Teilmenge der auftretenden Prädikatszeichen, so daß eine Theorie resultiert.

Denken wir zur Illustration hierfür nochmal an das oben geschilderte Beispiel mit der Eiscreme. Wir haben ja nun gesehen, daß die AWA die Minimierung der Interpretationsbereiche (im mengentheoretischen Sinne) der auftretenden Prädikate zum Ziel hat. Das Beispiel illustriert aber, daß es einem oft nur um die Minimierung (in diesem Sinne) von einigen der Prädikate geht. Hier ist es das Prädikat ``Abnormal'', das es zu minimieren gilt, weil wir grundsätzlich zunächst von normalen Dingen ausgehen und Abnormalität nur annehmen, wenn sie zwingend erforderlich ist, also in diesem Sinne Abnormalität minimieren. Beim Prädikat ``Liebt_Eiscreme'' hingegen gibt es (abgesehen von gesundheitlichen Bedenken) keine Veranlassung zu einer Minimierung. In der Tat ergibt sich in diesem Beispiel kein Widerspruch mehr, wenn die AWA nur auf Grundformeln mit dem Prädikat ``Abnormal'' angewendet wird.

Dieses Beispiel mag die Idee nahelegen, man müsse nur eine Untermenge der auftretenden Prädikate derart bestimmen und minimieren, daß dann die Formel ohne diese minimierten Atome Horn wird. Leider gibt es aber auch hierfür Gegenbeispiele [Sch90].

Wir haben bislang noch nicht darüber gesprochen, wie bei gegebener Wissensbank die Berücksichtigung der AWA tatsächlich realisiert wird. In [Rei77] hat Reiter ein Verfahren angegeben, das im Falle einer quantorenfreien Anfrage an die Wissensbank nur die in selbst enthaltenen Formeln berücksichtigt (vorausgesetzt ist konsistent). Es muß also die Menge der negierten nichtfolgerbaren Grundatomformeln nicht explizit aufgezählt werden. Besteht die Wissensbank nur aus Hornformeln, dann haben negative Klauseln (wie die Elemente von ) keinen Einfluß auf den Ableitungsprozess unter der Annahme der Weltabgeschlossenheit.

Die diskutierten Probleme des ursprünglichen Formalismus zur Modellierung der Annahme der Weltabgeschlossenheit haben zu etlichen Weiterentwicklungen geführt. Einer der ersten Ansätze wurde von Minker in [Min82] vorgestellt. Sein Ansatz wird als generalisierte Annahme der Weltabgeschlossenheit bezeichnet. Dieser Ansatz wurde in Form der vorsichtigen Annahme der Weltabgeschlossenheit von Gelfond und Przymusinska in [GP86] verallgemeinert. Die bisher allgemeinste Form der AWA stellt die von Gelfond, Przymusinska und Przymusinski in [GPP89] entwickelte erweiterte Annahme der Weltabgeschlossenheit dar. Insbesondere subsumiert diese die drei zuvor entwickelten Ansätze. In [Kat90] werden Modifikationen der AWA betrachtet, bei denen unter den Prädikatszeichen eine Präzedenzordnung angenommen wird. Dies führt zu einer partiellen, einer hierarchischen und einer schrittweisen AWA .

Wir erwähnen abschließend, daß die Annahme der Namenseindeutigkeit (engl. unique name assumption) als derjenige Spezialfall der AWA angesehen werden kann, bei der das Gleichheitsprädikat minimiert wird [Lif85a]. In den folgenden Abschnitten wird sich nun zeigen, daß die hier besprochenen Ideen und Konzepte in variierter, meist komplizierterer Form immer wieder auftauchen. Es ist besonders auch aus diesem Grunde, daß wir der AWA einen solch breiten Raum gewidmet haben.