Nächste Seite: 2.7 Terminologische Systeme Vorige Seite: 2.6.3 Eigenschaften der skeptischen

2.6.4 Das logische Analogon zur Vererbung

``There is nothing in ordinary logic very close in meaning to generic statements [ ]. In particular, `Birds fly' cannot be interpreted through a universally quantified formula of the form , and `Mammals don't fly' does not mean anything like '', stellen die Autoren von [HTT90] fest. Hier wollen wir zeigen, daß generische Aussagen nach unserer Auffassung quantifizierte Aussagen genau der in diesem Zitat wiedergegebenen Form sind. Insoweit stimmen wir mit der zitierten Aussage nicht überein. Im Falle des Auftretens von Widersprüchen während der Durchführung des Inferenzmechanismus müssen wir diesen allerdings zu einem ``nichtklassischen'' Verhalten veranlassen, das wir im folgenden erläutern werden. Das Zitat ist also insoweit richtig, als die klassische Inferenz nicht blind übertragen werden kann.

Betrachten wir hierzu nochmals das in Abbildung 2.17 wiedergegebene Netz zusammen mit der dort gegebenen Interpretation des nichtfliegenden Pinguins Zwitschi. Nach unserer Auffassung repräsentiert es die folgende Formel, in der wir die selbstverständlichen Allquantoren der Einfachheit halber weglassen.

In der Tat führt diese Theorie zu Widersprüchen, da ohne weitere Vorkehrungen die Aussage ableitbar ist, wie der in Abbildung 2.21 gezeigte Konnektionsbeweis (vgl. Abschnitt 2.3) demonstriert.

Abbildung 2.21: Nichtfliegende Pinguine als Formel

In dieser Situation standen wir aber in genau der gleichen Weise am Beginn der Behandlung der Vererbungsnetze. Dort haben wir schließlich einen Mechanismus angeben können, der es uns erlaubte, eine der beiden möglichen widersprüchlichen Schlußketten auszuschließen. Exakt der gleiche Mechanismus läßt sich in die logische Repräsentation in naheliegender Weise übersetzen. Denn offensichtlich entsprechen grob den Klassenknoten des Netzes dort die Konnektionen hier, während die Kanten dort hier durch die Klauseln repräsentiert sind. Die Gegenüberstellung ist durch die Abbildung 2.22 illustriert.

Abbildung 2.22: Eine Matrix und ihr zugehöriges Vererbungsnetz

In der Abbildung ist die gleiche Matrix des vorangegangenen Beispiels dargestellt. Da wir es in der Sprache der Vererbungsnetze jedoch ausschließlich mit einstelligen Prädikaten zu tun haben, verstehen sich die variablen Argumente von selbst und wurden daher in der Darstellung nicht mehr explizit gezeigt. Außerdem unterscheidet sich die abgemagerte Matrix von der in Abbildung 2.21 durch einen Knoten in jeder Konnektion. Im einzelnen entsprechen also den Kanten , , und die Matrixstücke

Schließlich ist hier die Zielklausel nicht explizit aufgeführt, da auch sie aus dem Kontext erschlossen werden kann. Die Gegenüberstellung macht deutlich, daß Netze die gleiche Information wesentlich komprimierter kodieren als Formeln oder Matrizen.

Um die Kompaktheit der Netze im Vergleich zu Formeln noch augenfälliger zu illustrieren, sind in Abbildung 2.23 der in Abschnitt 2.3 erklärte gaG einer Formel und das entsprechende Netz einander gegenübergestellt.

Abbildung 2.23: Der gaG einer Formel und das zugehörige Netz

Nachdem hiermit die Entsprechung der logischen Formel mit dem Netz geklärt ist, mag sich der Leser die Frage stellen, warum logische Formeln nicht immer so vereinfacht dargestellt werden, wie es durch Netze ganz offensichtlich geschieht. Der Grund liegt natürlich in den radikal einschränkenden Annahmen, auf denen Netze beruhen und die in komplizierteren Fällen leider nicht mehr erfüllt sind. Netze behandeln nämlich ausschließlich einstellige Prädikate sowie Regeln mit lediglich einer Prämisse und einer Konklusion, ein extrem spezieller Fall. Formeln dagegen sind auch für den allgemeinsten Fall zu dessen Darstellung gewappnet und genau aus diesem Grunde verständlicherweise komplexer in ihrer Repräsentation.

Mit dieser Diskussion haben wir das von Frege eingeführte Formelkonzept nicht wirklich ins rechte Licht gerückt. Viel zu wenig wird nämlich daran gedacht, das Werkzeug des bereits von Frege selbst ins Auge gefaßten Definitionsmechanismus bei der Formelbildung mit einzusetzen. So läßt sich als Abkürzung für definieren. Alternativ läßt sich diese verallgemeinerte Implikation mit Hilfe des 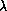-Mechanismus in der Form zusammen mit definieren. In gleicher Weise ergeben sich die Definitionen für den Fall mehrerer Implikationsglieder. Diese Definitionen vorausgesetzt, reduziert sich die verbleibende Formel ebenfalls auf wie im Falle des Netzes.

Man mag einwenden, daß hier der Ballast nur in die Definition verschoben wird, die ja als Prämisse ein für allemal in die Gesamtformel miteinbezogen werden muß. Das ist zwar richtig, gilt aber für den Netzmechanismus in gleicher Weise. Nur ist dieser Teil der formalen Beschreibung der Netzstruktur üblicherweise als informelle Erklärung im kursiven Text zu finden, während man mit dem logischen Apparat die Formalisierung mit großem Gewinn meist ein Stück weitertreibt. Kurz und bündig, der vermeintliche Vorteil der Netzdarstellung hat sich in nichts aufgelöst; wir haben nur das wichtige, von der Logik gebotene Mittel der Definition ignoriert.

Mit der gegebenen Entsprechung sind nun auch die im Zusammenhang der Netze eingeführten Begriffe unmittelbar und wortwörtlich auf logische Formeln übertragbar, allen voran der Begriff eines Pfades. Auf diese Weise macht es dann einen Sinn, davon zu sprechen, daß ein Pfad in einer Matrix erlaubt ist. Danach ist der Pfad, der die Aussage stützen würde, eben nicht erlaubt, genausowenig wie im Fall der Netzdarstellung. Diese Lösung hat demnach im Licht der Logik die folgende Erklärung.

Eine Formel oder Matrix, die wie die obige logisch gesehen widersprüchlich ist, stellt eigentlich eine Kombination mehrerer Formeln dar, die Teile gemeinsam haben. In unserem Beispiel der Abbildung 2.21 handelt es sich um zwei solche Formeln, deren Matrizen in der Abbildung 2.24 gezeigt sind. Man beachte, daß die Überlagerung der beiden Matrizen wieder die ursprüngliche Matrix ergibt. Jede der beiden Matrizen ist in sich widerspruchsfrei, erst ihre Kombination führt zum Widerspruch. Zum Beweis einer gegebenen Anfrage wird nun immer nur eine der beiden Matrizen herangezogen. Um in Konfliktfällen entscheiden zu können, welche der beiden zu wählen ist, haben wir in diesem Abschnitt die Technik der erlaubten Pfade entwickelt.

Abbildung 2.24: Die Überlagerungsmatrizen der Abbildung 2.21

Zusammenfassend können wir also das Folgende sagen. Vererbungsnetze sind kompakte Darstellungen von Formeln einer sehr eingeschränkten Klasse. Überdies erlauben sie die Überlagerung mehrerer Formeln, die einzeln konsistent sind, überlagert jedoch zu Widersprüchen führen. Der in diesem Abschnitt entwickelte Mechanismus erlaubt, bei einer gegebenen deduktiven Problemstellung eindeutig eine dieser konsistenten Teilformeln zu bestimmen, mittels der sich die Lösung dann in der in der Logik üblichen Weise ergibt. Durch den so mit der Logik hergestellten Zusammenhang ist es möglich, den Vererbungsmechanismus auch innerhalb komplizierterer Problemklassen, als sie durch Netze gegeben sind, einzubetten, wobei die in diesem Abschnitt besprochenen Techniken der Konfliktauflösung dann natürlich nur auf der Teilklasse von Formeln anwendbar sind, für die sie theoretisch gesichert sind. Andere Inferenzformen (wie die der klassischen Inferenz) sind dann aber auf die gesamte Problemklasse anwendbar.