





Der Ableitbarkeitsbegriff in der Ermangelungslogik weicht so stark von dem der klassischen Logik ab, daß die ``Bedeutung'' der Ableitbarkeit einer Formel keineswegs mehr offensichtlich ist. Die Frage nach der Semantik der Ermangelungslogik ist daher alles andere als trivial und hat mehr als ein Jahrzehnt eine Reihe von Forschern intensiv beschäftigt. In diesem Unterabschnitt wollen wir daher eine solche Semantik angeben.
Beginnen wir zunächst damit, an die Semantik der Prädikatenlogik (siehe
Abschnitt 2.3) zu erinnern [Bib87a, Sho67]. Sie gründet sich
auf den Begriff der Interpretation. Mittels einer Interpretation wird jeder
Formel über dem betrachteten Alphabet ein
Wahrheitswert zugeordnet.
Betrachten wir zB. die Menge ![]() der Fakten einer Ermangelungstheorie, so
erhält jedes dieser Fakten in einer solchen Interpretation den Wert wahr
oder falsch. Wenn unter einer gegebenen Interpretation alle Fakten den Wert
wahr erhalten, dann nennt man diese Interpretation ein Modell der Faktenmenge.
Hat man ein solches Modell der Faktenmenge, so ist auch jede aus
der Fakten einer Ermangelungstheorie, so
erhält jedes dieser Fakten in einer solchen Interpretation den Wert wahr
oder falsch. Wenn unter einer gegebenen Interpretation alle Fakten den Wert
wahr erhalten, dann nennt man diese Interpretation ein Modell der Faktenmenge.
Hat man ein solches Modell der Faktenmenge, so ist auch jede aus ![]() klassisch ableitbare Formel in dieser Interpretation wahr; die Interpretation
ist also auch ein Modell der abgeleiteten Formel. Jedes Modell der Faktenmenge
ist daher ebenso ein Modell aller aus ihr klassisch ableitbaren Formeln.
klassisch ableitbare Formel in dieser Interpretation wahr; die Interpretation
ist also auch ein Modell der abgeleiteten Formel. Jedes Modell der Faktenmenge
ist daher ebenso ein Modell aller aus ihr klassisch ableitbaren Formeln.
Genau diese zuletzt genannte Eigenschaft geht in der Ermangelungslogik
verloren. Denken wir wieder an unser Standardbeispiel, und nehmen wir also an,
daß die Menge der Fakten nur aus ![]() besteht und
besteht und
![]()
als einzige Regel gegeben ist. Durch Anwendung der Ermangelungsregel können
wir auf die Formel ![]() schließen. Die Modelle unserer Faktenmenge
sind dadurch charakterisiert, daß sie alle die Formel
schließen. Die Modelle unserer Faktenmenge
sind dadurch charakterisiert, daß sie alle die Formel ![]() erfüllen, dh. wahr machen. Unter ihnen sind daher auch solche, die die
abgeleitete Formel
erfüllen, dh. wahr machen. Unter ihnen sind daher auch solche, die die
abgeleitete Formel ![]() falsch machen, dh. diese Modelle sind, anders
als in der klassischen Logik, keine Modelle dieser abgeleiteten Formel. Durch
die Anwendung der Ermangelungsregel wird die Menge der Modelle der Faktenmenge
offensichtlich eingeschränkt, dh. es werden weniger Modelle, als ohne die
Anwendung der Regel vorhanden sind.
falsch machen, dh. diese Modelle sind, anders
als in der klassischen Logik, keine Modelle dieser abgeleiteten Formel. Durch
die Anwendung der Ermangelungsregel wird die Menge der Modelle der Faktenmenge
offensichtlich eingeschränkt, dh. es werden weniger Modelle, als ohne die
Anwendung der Regel vorhanden sind.
In einer ersten Näherung kann man also sagen, daß die in einer Ermangelungstheorie ableitbaren Formeln semantisch durch eine Teilmenge der Modellmenge zur Faktenmenge bestimmt ist. Unser Ziel ist es, die Teilmenge so zu bestimmen, daß jedes Modell dieser Teilmenge auch ein Modell einer Extension der Ermangelungstheorie in dem Sinne ist, daß alle Formeln der Extension unter der zugrundeliegenden Interpretation wahr sind. Wir haben bereits im vorangegangenen Unterabschnitt gesehen, daß es mehrere Extensionen geben kann. Es kann daher auch sein, daß eine solche Teilmenge nicht eindeutig bestimmt ist; vielmehr kann es also auch mehr als eine derartige Teilmenge geben, und zwar zu jeder Extension genau eine.
Damit stehen wir nun vor der entscheidenden Frage, wie nämlich diese Teilmengen semantisch charakterisierbar sind. Die Antwort auf diese Frage fußt auf zwei entscheidenden Ideen. Die eine Idee beruht auf der Einführung einer Präferenzrelation auf Modellmengen, die durch die Ermangelungsregeln bestimmt ist. Auf sie werden wir weiter unten zu sprechen kommen. Die andere Idee fußt auf der Betrachtung von Kripke-Modellen anstelle von prädikatenlogischen Modellen. Diese Idee wurde zuerst in [BS92] realisiert und soll uns nun beschäftigen.
Hierzu erinnern wir zunächst an den in Abschnitt 2.11.7
eingeführten Begriff eines Kripke-Modells. Es besteht aus einer Menge
möglicher Welten,
unter denen eine aktuelle Welt ausgezeichnet ist. Zu jeder
dieser Welten gibt es eine (prädikatenlogische) Interpretation, so daß
wir vom Wahrheitswert einer Formel in einer Welt sprechen können.
Schließlich ist die Menge der Welten durch eine
Erreichbarkeitsrelation
strukturiert, so daß man von einer Welt eine andere erreichen bzw. nicht
erreichen kann. Eine Formel der Gestalt ![]() ist dann in der aktuellen
Welt wahr, wenn
ist dann in der aktuellen
Welt wahr, wenn ![]() in allen von ihr aus erreichbaren Welten wahr ist,
während
in allen von ihr aus erreichbaren Welten wahr ist,
während ![]() dann wahr ist, wenn es eine erreichbare Welt gibt,
in der
dann wahr ist, wenn es eine erreichbare Welt gibt,
in der ![]() wahr ist;
wahr ist; ![]() selbst ist wahr, wenn
selbst ist wahr, wenn ![]() in der
aktuellen Welt wahr ist.
in der
aktuellen Welt wahr ist.
Zum Verständnis der Idee der Verwendung von Kripke-Modellen stellen wir uns
die Erreichbarkeitsrelation zunächst wie folgt vor: Eine Welt ![]() ist
dann aus einer Welt
ist
dann aus einer Welt ![]() erreichbar, wenn in
erreichbar, wenn in ![]() alles gilt, was in
alles gilt, was in
![]() gilt. Intuitiver können wir das auch so formulieren, daß
gilt. Intuitiver können wir das auch so formulieren, daß
![]() die aktuelle Welt darstellt, die alle meine Überzeugungen
widerspiegelt (zB. daß Larissa ein Kind ist), während
die aktuelle Welt darstellt, die alle meine Überzeugungen
widerspiegelt (zB. daß Larissa ein Kind ist), während ![]() eine
vorgestellte Welt ist, in der über mir unklare Sachverhalte zusätzliche
Annahmen getroffen sind (zB. daß Larissa blond ist). Betrachten wir dazu
die in Abbildung 3.3 gezeigte Kripke-Struktur, die aus vier Welten besteht.
eine
vorgestellte Welt ist, in der über mir unklare Sachverhalte zusätzliche
Annahmen getroffen sind (zB. daß Larissa blond ist). Betrachten wir dazu
die in Abbildung 3.3 gezeigte Kripke-Struktur, die aus vier Welten besteht.
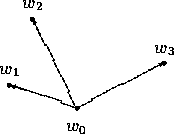
Abbildung 3.3: Ein Kripke-Modell bestehend aus vier Welten.
In der aktuellen Welt ![]() sei
sei ![]() wahr. Weiter nehmen wir nun an,
daß
wahr. Weiter nehmen wir nun an,
daß ![]() auch in
auch in ![]() und
und ![]() wahr ist. Deshalb sind
unter der eben beschriebenen Vorstellung der Erreichbarkeit diese drei Welten
aus der aktuellen Welt erreichbar, genau wie es die Abbildung zeigt.
Tatsächlich ist in dieser Vorstellung auch noch
wahr ist. Deshalb sind
unter der eben beschriebenen Vorstellung der Erreichbarkeit diese drei Welten
aus der aktuellen Welt erreichbar, genau wie es die Abbildung zeigt.
Tatsächlich ist in dieser Vorstellung auch noch ![]() aus
aus ![]() erreichbar, was in der Abbildung nicht explizit gezeigt ist. Wir nehmen nun
zusätzlich an, daß die Formel
erreichbar, was in der Abbildung nicht explizit gezeigt ist. Wir nehmen nun
zusätzlich an, daß die Formel ![]() in
in ![]() und
und ![]() wahr
und in
wahr
und in ![]() und
und ![]() falsch ist.
falsch ist.
Nach diesen Vorbemerkungen kommen wir nun zur Motivation, warum sich
Kripke-Modelle zur Beschreibung der Semantik einer Ermangelungstheorie besonders
eignen. Denken wir uns nämlich ![]() als die Konklusion einer erfolgreich
angewendeten Ermangelungsregel mit der Rechtfertigung
als die Konklusion einer erfolgreich
angewendeten Ermangelungsregel mit der Rechtfertigung ![]() . Dann ist
. Dann ist
![]() in der aktuellen Welt wahr, da wir ja immer annehmen, daß die
Fakten in der aktuellen Welt
in der aktuellen Welt wahr, da wir ja immer annehmen, daß die
Fakten in der aktuellen Welt ![]() gelten und erfolgreiche Anwendungen von
Ermangelungsregeln zu wahren Aussagen über die aktuelle Welt führen. Dann
muß aber
gelten und erfolgreiche Anwendungen von
Ermangelungsregeln zu wahren Aussagen über die aktuelle Welt führen. Dann
muß aber ![]() auch in allen Welten wahr sein, die wir uns vorstellen
können, dh. die von
auch in allen Welten wahr sein, die wir uns vorstellen
können, dh. die von ![]() aus erreichbar sind; modallogisch besagt
dies, daß auch
aus erreichbar sind; modallogisch besagt
dies, daß auch ![]() wahr ist. Zudem muß die Rechtfertigung
wahr ist. Zudem muß die Rechtfertigung
![]() der Regel als Annahme möglich sein; mit anderen Worten,
der Regel als Annahme möglich sein; mit anderen Worten, ![]() muß mit den Überzeugungen, die
muß mit den Überzeugungen, die ![]() prägen, vereinbar sein in dem
Sinne, daß wir uns eine Welt vorstellen können (dh. die erreichbar
ist) in der (nicht nur
prägen, vereinbar sein in dem
Sinne, daß wir uns eine Welt vorstellen können (dh. die erreichbar
ist) in der (nicht nur ![]() , sondern auch)
, sondern auch) ![]() gilt; dieses wiederum
besagt modallogisch
gilt; dieses wiederum
besagt modallogisch ![]() . Insgesamt ergibt sich also, daß die
angenommene Kripke-Struktur (wie die in Abbildung 3.3 gezeigte) ein
Kripke-Modell der Formeln
. Insgesamt ergibt sich also, daß die
angenommene Kripke-Struktur (wie die in Abbildung 3.3 gezeigte) ein
Kripke-Modell der Formeln ![]() und
und ![]() , also auch von
, also auch von
![]() ist. Tatsächlich ist diese Formel auch
in der Struktur der Abbildung 3.3 mit den oben beschriebenen
Interpretationen wahr. Genau diese Formel wird ein entscheidender Baustein der
unten stehenden Definition sein.
ist. Tatsächlich ist diese Formel auch
in der Struktur der Abbildung 3.3 mit den oben beschriebenen
Interpretationen wahr. Genau diese Formel wird ein entscheidender Baustein der
unten stehenden Definition sein.
Diese Überlegungen zeigen, in welch natürlicher Weise sich eine
ermangelungslogisch abgeleitete Formel ![]() mittels eines Kripke-Modells
semantisch fassen läßt. Dies wollen wir nun formal für eine beliebige
Ermangelungstheorie
mittels eines Kripke-Modells
semantisch fassen läßt. Dies wollen wir nun formal für eine beliebige
Ermangelungstheorie ![]() durchführen.
durchführen.
Wir beginnen mit den Fakten ![]() . Eingangs sind wir von der Menge von
Modellen von
. Eingangs sind wir von der Menge von
Modellen von ![]() ausgegangen. Wie wir jetzt gesehen haben, ist es nötig,
anstelle klassischer Modelle nun die Menge von Kripke-Modellen von
ausgegangen. Wie wir jetzt gesehen haben, ist es nötig,
anstelle klassischer Modelle nun die Menge von Kripke-Modellen von ![]() ins
Auge zu fassen, was in der folgenden Definition zum Ausdruck kommt.
ins
Auge zu fassen, was in der folgenden Definition zum Ausdruck kommt.
![]()
SeiMit den folgenden Bemerkungen wollen wir diese Definition noch vertrauter machen. In ihr verwenden wir, wie üblich, die Bezeichnungeine Ermangelungstheorie{Theorie!Ermangelungs~} und
die Menge der Kripke-Strukturen
, wobei von
keine speziellen Eigenschaften verlangt werden (die zugrundeliegende Modallogik also das modallogische System
ist -- siehe Abschnitt 2.11.7). Dann ist die mit
assoziierte Klasse von Kripke-Modellen {Klasse!assoziierte Kripke-Modell~} definiert als
.
 wahr ist. Wie ersichtlich, handelt es
sich hier um die oben besprochene Formel
wahr ist. Wie ersichtlich, handelt es
sich hier um die oben besprochene Formel
Wie bei einer klassischen Formel gehen wir auch hier von der Menge
aller Kripke-Modelle zur semantischen Charakterisierung von ![]() aus.
Dabei schränken wir
aus.
Dabei schränken wir ![]() in keiner Weise ein; dh. insbesondere, daß
die oben suggerierte Vorstellung von
in keiner Weise ein; dh. insbesondere, daß
die oben suggerierte Vorstellung von ![]() nur eine von vielen ist. Um den
Vergleich mit dem klassischen Fall noch weiter zu vertiefen, sei darauf
hingewiesen, daß es zu jedem klassischen Modell
nur eine von vielen ist. Um den
Vergleich mit dem klassischen Fall noch weiter zu vertiefen, sei darauf
hingewiesen, daß es zu jedem klassischen Modell ![]() von
von ![]() eine
ganze Menge von Kripke-Modellen gibt, die sich in der Menge
eine
ganze Menge von Kripke-Modellen gibt, die sich in der Menge ![]() der Welten,
in der Interpretationsfunktion oder in der Erreichbarkeitsrelation
der Welten,
in der Interpretationsfunktion oder in der Erreichbarkeitsrelation ![]() unterscheiden und nur in der aktuellen Welt übereinstimmen, dh. es gilt
unterscheiden und nur in der aktuellen Welt übereinstimmen, dh. es gilt
![]() für jede der Strukturen.
für jede der Strukturen.
Wir sprachen oben davon, daß die Antwort auf die Frage der Charakterisierung der zu einer Extension gehörigen Teilmenge von (Kripke-) Modellen auf zwei Ideen fußt, von denen wir die der Kripke-Modelle nun ausführlich besprochen haben. Die zweite Idee beruht auf der Einführung einer Präferenzrelation zwischen verschiedenen Kripke-Modellmengen, die für den Fall klassischer Modelle zum erstenmal in [Eth88] verwendet wurde. Wir geben zunächst die formale Definition und dann eine Reihe von Erläuterungen dazu.
![]()
SeiZur Erläuterung dieser Definition bedienen wir uns wieder des Standarbeispiels mit der Faktenmengeeine Ermangelungstheorie und
. Zu zwei verschiedenen Klassen M und
von Kripke-Strukturen, für die
erfüllt ist, gelte
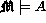
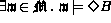
genau dann, wenn

Für eine Menge
von Ermangelungsregeln definieren wir die strikte partielle Ordnung
als die transitive Hülle der Vereinigung aller
mit
. Wir bezeichnen dann die
-maximalen Klassen von Kripke-Modellen über
als die präferierten Klassen von Kripke-Modellen zu
.
![]()
Voraussetzung für die Ermittlung einer Menge ![]() , für die
, für die
![]() , nach Definition 3.7.2 gilt, ist das
Erfülltsein der beiden in der Definition genannten Bedingungen. Erstens
muß die Voraussetzung
, nach Definition 3.7.2 gilt, ist das
Erfülltsein der beiden in der Definition genannten Bedingungen. Erstens
muß die Voraussetzung ![]() der Regel in allen Modellen von
der Regel in allen Modellen von
![]() gelten, dh.
gelten, dh. ![]() , was
nach Definition von
, was
nach Definition von ![]() gegeben ist. Zweitens muß
gegeben ist. Zweitens muß
![]() möglich sein, dh. unter den Modellen von
möglich sein, dh. unter den Modellen von ![]() muß es eines geben, in dem es eine erreichbare
(vorstellbare) Welt gibt, in der
muß es eines geben, in dem es eine erreichbare
(vorstellbare) Welt gibt, in der ![]() wahr ist. Da die Definition von
wahr ist. Da die Definition von
![]() alle denkbaren Kripke-Modelle umfaßt, ist in
alle denkbaren Kripke-Modelle umfaßt, ist in
![]() auch dasjenige Modell
auch dasjenige Modell ![]() , das aus den beiden Welten
, das aus den beiden Welten
![]() und
und ![]() besteht, wobei in diesen beiden Welten die Literale
besteht, wobei in diesen beiden Welten die Literale
![]() und
und ![]() wahr sind und
wahr sind und ![]() aus
aus ![]() erreichbar
ist; denn für dieses Modell gilt offensichtlich
erreichbar
ist; denn für dieses Modell gilt offensichtlich ![]() , wie es Definition 3.7.2 vorschreibt. Nach
Konstruktion gilt nun aber auch
, wie es Definition 3.7.2 vorschreibt. Nach
Konstruktion gilt nun aber auch ![]() .
.
Um es nochmals allgemein zu formulieren, kann es zu einer Regel ![]() und einer Kripke-Modellmenge
und einer Kripke-Modellmenge ![]() nur dann eine Menge
nur dann eine Menge ![]() mit
mit ![]() geben, wenn die Voraussetzung
geben, wenn die Voraussetzung
![]() von
von ![]() in allen Modellen von
in allen Modellen von ![]() gilt und wenn die
Rechtfertigung
gilt und wenn die
Rechtfertigung ![]() von
von ![]() möglich ist, dh. in mindestens
einem Modell gilt.
möglich ist, dh. in mindestens
einem Modell gilt.
Sind diese beiden Bedingungen erfüllt, dann präferiert ![]() bezüglich
bezüglich ![]() diejenige Teilmenge
diejenige Teilmenge ![]() von Modellen,
dh.
von Modellen,
dh. ![]() , in denen also
, in denen also ![]() gilt und
notwendigerweise gilt und
gilt und
notwendigerweise gilt und ![]() möglich ist, in denen nun aber
zusätzlich auch die Folgerung
möglich ist, in denen nun aber
zusätzlich auch die Folgerung ![]() von
von ![]() gilt, und zwar auch
notwendigerweise. Im Beispiel ergibt sich für
gilt, und zwar auch
notwendigerweise. Im Beispiel ergibt sich für
![]()
also ![]() . In
. In ![]() gilt mehr als in
gilt mehr als in ![]() , in welchem Sinne das
, in welchem Sinne das ![]() -Zeichen zu
lesen ist (denn als Menge ist
-Zeichen zu
lesen ist (denn als Menge ist ![]() ja kleiner als
ja kleiner als ![]() ).
).
Im allgemeinen gibt es nun mehr als eine Regel in der Regelmenge ![]() .
Hierzu sagt die Definition 3.7.2, daß wir ignorieren, durch welches
.
Hierzu sagt die Definition 3.7.2, daß wir ignorieren, durch welches
![]() eine Menge
eine Menge ![]() präferiert wurde; dh. wann immer
präferiert wurde; dh. wann immer
![]() , dann auch
, dann auch ![]() . Außerdem verlangen wir von
. Außerdem verlangen wir von ![]() die Eigenschaft der
Transitivität.
die Eigenschaft der
Transitivität.
Zur Bildung einer zu einer Ermangelungstheorie ![]() gehörigen
präferierten Kripke-Modellmenge gehen wir schließlich aus von
gehörigen
präferierten Kripke-Modellmenge gehen wir schließlich aus von ![]() , bilden
, bilden ![]() und wählen ein bezüglich dieser Relation
maximales Modell. Eine solche präferierte Modellmenge charakterisiert die
Menge
und wählen ein bezüglich dieser Relation
maximales Modell. Eine solche präferierte Modellmenge charakterisiert die
Menge ![]() derjenigen Formeln, die in allen aktuellen Welten dieser Modelle
wahr sind. Damit haben wir die gewünschte semantische Charakterisierung der
Formelmenge gegeben, die unsere Überzeugungen formuliert und nach der wir am
Beginn dieses Unterabschnitts gefragt haben.
derjenigen Formeln, die in allen aktuellen Welten dieser Modelle
wahr sind. Damit haben wir die gewünschte semantische Charakterisierung der
Formelmenge gegeben, die unsere Überzeugungen formuliert und nach der wir am
Beginn dieses Unterabschnitts gefragt haben.
In unserem Beispiel besteht ![]() lediglich aus
lediglich aus ![]() und dieses aus dem Paar
und dieses aus dem Paar ![]() .
.
![]() ist also das einzige maximale Element und daher die
präferierte Kripke-Modellmenge unseres Beispiels. In ihr gilt
ist also das einzige maximale Element und daher die
präferierte Kripke-Modellmenge unseres Beispiels. In ihr gilt ![]() , die einzig mögliche Extension unseres Beispiels.
, die einzig mögliche Extension unseres Beispiels.
Darüber hinaus charakterisiert eine präferierte Kripke-Modellmenge nicht nur
die Menge unserer Überzeugungen, sondern macht in den aus ![]() erreichbaren Welten der Modelle auch alle impliziten Annahmen
erreichbaren Welten der Modelle auch alle impliziten Annahmen ![]() explizit, auf denen diese Überzeugungen beruhen.
explizit, auf denen diese Überzeugungen beruhen.
In [Sch92] findet sich der formale Beweis dafür, daß es zu jeder
Extension ![]() einer Ermangelungstheorie
einer Ermangelungstheorie ![]() eine
präferierte Modellmenge
eine
präferierte Modellmenge ![]() gibt, in der
gibt, in der ![]() gilt, und daß
es zu jeder präferierten Modellmenge
gilt, und daß
es zu jeder präferierten Modellmenge ![]() eine Extension
eine Extension ![]() gibt, die in
gibt, die in ![]() gilt. Es handelt sich dabei also um eine Art
Korrektheits- und Vollständigkeitssatz für die Ermangelungslogik, der wie
folgt lautet.
gilt. Es handelt sich dabei also um eine Art
Korrektheits- und Vollständigkeitssatz für die Ermangelungslogik, der wie
folgt lautet.
![]()
SeiNeben der hier beschriebenen Semantik der Ermangelungslogik finden sich in der Literatur noch andere. Eine erste semantische Charakterisierung der Ermangelungslogik wurde in [Luk84] für normale Ermangelungstheorien angegeben. Die erste Semantik für allgemeine Ermangelungstheorien wurde in [Eth88] beschrieben. Wie bereits weiter oben erwähnt, führte Etherington dazu eine durch Ermangelungsregeln induzierte Präferenzrelation zwischen Klassen von Modellen einer betrachteten Faktenmengeeine abgeschlossene Ermangelungstheorie. Sei
eine Klasse von Kripke-Modellen und
eine deduktiv abgeschlossene Menge von Sätzen, so daß
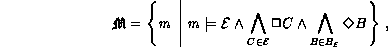
wobei
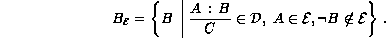
Dann ist
eine konsistente Extension von
genau dann, wenn M eine
-maximale, nicht-leere Klasse über
ist.
Ein zusätzlicher Vorteil der hier präsentierten Semantik ist ihre
Allgemeinheit. Tatsächlich stellt sie einen Rahmen dar, mit dem verschiedene
in der Literatur betrachtete Ermangelungslogiken in einheitlicher Weise
semantisch charakterisiert werden können. Neben der Reiterschen
Ermangelungslogik sind hier zB. eine Variante von
![]() ukaszewicz [Luk88], die kumulative
Ermangelungslogik
von
Brewka [Bre91a] und die bedingten
Ermangelungslogiken
von Delgrande und
Jackson [DJ91] sowie von
Schaub [Sch92] zu nennen. Damit werden die Bezüge
dieser unterschiedlichen Logiken aus semantischer Sicht verständlich und
durchsichtig. Auch fügen sich alle bisher betrachteten Semantiken in diesen
Rahmen ein, soweit sie auf der Idee einer Präferenzrelation beruhen. In
diesem Sinne fällt die in [dGC90] betrachtete Semantik aus dem
Rahmen.
ukaszewicz [Luk88], die kumulative
Ermangelungslogik
von
Brewka [Bre91a] und die bedingten
Ermangelungslogiken
von Delgrande und
Jackson [DJ91] sowie von
Schaub [Sch92] zu nennen. Damit werden die Bezüge
dieser unterschiedlichen Logiken aus semantischer Sicht verständlich und
durchsichtig. Auch fügen sich alle bisher betrachteten Semantiken in diesen
Rahmen ein, soweit sie auf der Idee einer Präferenzrelation beruhen. In
diesem Sinne fällt die in [dGC90] betrachtete Semantik aus dem
Rahmen.






Christoph Quix, Thomas List, René Soiron