Nächste Seite: 3.7.2 Die Semantik der Vorige Seite: 3.7 Eine Ermangelungslogik

3.7.1 Die Syntax der Ermangelungslogik

Wie beim Ansatz mittels Theoriebildung, den wir im letzten Abschnitt besprochen haben, werden auch in der Ermangelungslogik die Faust- oder Ermangelungsregeln innerhalb der gegebenen Weltbeschreibung gesondert behandelt. Auch hier unterscheiden wir also zwischen den Fakten , einer Menge geschlossener Formeln, und dem, was wir im vorangegangenen Abschnitt als die möglichen Hypothesen bezeichnet haben. Dieser letztere Teil wird nun hier aber zur Definition einer veränderten Logik herangezogen, und nicht, wie dort, zur Bildung einer konsistenten Theorie.

Betrachten wir unser altes Beispiel der Eiscreme-liebenden Kinder , wobei das ``normalerweise'' in dieser Fassung der Regel noch nicht zum Ausdruck kommt. In der Ermangelungslogik erhält diese Regel unter Berücksichtigung des ``normalerweise'' die folgende Gestalt.

In Worten, wenn ableitbar ist, daß Kind ist, und nichts gegen die Annahme, liebt Eiscreme, spricht (dh. logisch, daß diese Annahme mit dem übrigen Wissen konsistent ist), dann läßt sich auch schlüssig folgern, daß Eiscreme liebt.

In dieser Gestalt ist (wie bei Gentzen) die Regel als Kalkülregel aufzufassen. Das heißt, wir gehen aus von irgendeinem (vollständigen) Kalkül der Prädikatenlogik erster Stufe und erweitern dessen Ableitungsregeln um diese zusätzliche Regel. Insbesondere ändern wir also den Kalkül, indem wir einen Teil unseres Wissens in stecken, während wir in allen bisherigen Ansätzen (mit Ausnahme der Annahme der Weltabgeschlossenheit AWA, die sich jetzt auch als Vorläufer der Ermangelungslogik auffassen läßt) die Logik selbst unangetastet ließen. Diese Kalküländerung hat eine irrelevante und eine relevante Komponente.

Aufgrund des Deduktionstheorems [Bib87a] ist äquivalent mit . Daß wir also eine in Form einer Implikationsregel im Wissen enthaltene Regel als Kalkülregel repräsentieren, macht noch keinen relevanten Unterschied; dies ist also die irrelevante Komponente. Der entscheidende Unterschied besteht in einer ganz neuartigen Form von Kalkülregeln. So muß zur Prüfung der Anwendbarkeit der obigen Regel erst die Menge aller aus in der bisherigen Weise ableitbaren Formeln daraufhin untersucht werden, ob sie enthält. Nur wenn das nicht der Fall ist, darf die Regel angewendet werden. Da die Ableitbarkeit in der Prädikatenlogik nicht entscheidbar ist, kann also auch die Anwendbarkeit einer solchen Regel im allgemeinen gar nicht entschieden werden, während die Anwendbarkeit von üblichen Kalkülregeln immer entscheidbar ist und sich auf die Prüfung der Prämissen reduziert.

Der soeben beschriebene relevante Anteil bildet das Gegenstück in der Ermangelungslogik zur Einführung von Abnormalitätsprädikaten und deren Minimierung, wie es bei der Zirkumskription erfolgt. Bei letzterer bleibt alles unter der expliziten Kontrolle des Logikprogrammierers, während hier nun die Zügel dem Inferenzmechanismus überlassen bleiben, dessen einzige Schranken durch die geforderte Konsistenz gegeben werden. Hier handelt es sich also um ein wesentlich anderes Vorgehen. Es ist daher nicht verwunderlich, daß es einige Zeit gedauert hat, bis die Zusammenhänge zwischen diesen beiden Sichtweisen zur Nichtmonotonie weitgehend geklärt werden konnten [Kon88].

Wir werden nun diesen neuen Ansatz im einzelnen entwickeln. Insbesondere können die Regeln allgemeiner sein, als durch unser bisheriges Beispiel illustriert ist [Rei80].

Eine Ermangelungsregel (oder auch Faustregel; engl. default rule) ist eine Kalkülregel der Gestalt

wobei und Formeln der Prädikatenlogik erster Stufe sind. heißt die Voraussetzung, die Folgerung, und jedes heißt eine Rechtfertigung der Regel. Die Regel heißt abgeschlossen, wenn alle diese auftretenden Formeln keine freien Variablen enthalten.

Im gegenwärtigen Kontext werden wir oft kurz von Regel sprechen, wenn Mißverständnisse ausgeschlossen sind. In der ursprünglichen Fassung hat Reiter vor die noch jeweils einen Möglichkeitsoperator in der Form geschrieben (vgl. hierzu den nachfolgenden Abschnitt), was sich aber erübrigt. Eine Ermangelungstheorie ist dann in der oben beschriebenen Weise durch ein Paar gegeben, wobei eine Menge von geschlossenen Formeln, den Fakten, und eine Menge von Ermangelungsregeln sind, wobei die Mengen immer als höchstens abzählbar unendlich angenommen werden. Die Theorie heißt abgeschlossen, wenn dies alle Regeln sind. Eine offene Ermangelungsregel wird üblicherweise als Schema angesehen und repräsentiert daher die Menge aller ihrer Grundinstanzen.

Bei den so eingeführten Regeln gibt es eine Reihe von wichtigen Spezialfällen, die wir jetzt besprechen. So kann leer sein, was auch als die Formel true (bzw. als irgendeine Tautologie) angesehen werden kann. Der Fall ist in unserem Zusammenhang uninteressant, da es sich dann um eine herkömmliche Regel handelt. Im Falle unterscheiden wir die folgenden beiden Spezialfälle. Ist nämlich dann , so heißt die Regel normal, bzw. ist für irgendein , so heißt die Regel semi-normal. Praktisch fallen alle Beispiele in diese beiden Kategorien.

In der klassischen Logik wird sowohl eine Menge W von Axiomen als auch die Menge der ableitbaren Formeln als Theorie bezeichnet, weil der Bezug fixiert und eindeutig ist. Da wir nun einen veränderten Ableitungsbegriff haben und die Eindeutigkeit der Menge der ableitbaren Formeln nicht mehr gegeben ist (wie wir unten noch sehen werden), reservieren wir für die Menge der ableitbaren Formeln den Begriff einer Extension (oder Erweiterung). Man sei sich dabei der Problematik einer möglichen Zirkularität bewußt, denn die Ableitbarkeit ist über die Ermangelungsregel durch die Nicht-Ableitbarkeit und diese natürlich wieder durch die Ableitbarkeit selbst bedingt. Die folgende Fixpunktdefinition vermeidet den Zirkel.

Sei eine Ermangelungstheorie. Zu einer gegebenen Menge von Sätzen (dh. geschlossenen Formeln) betrachten wir die kleinste Menge von Sätzen, für die die folgenden drei Bedingungen erfüllt sind.

1. .
2. .
3. Für jede Regel gilt, wenn und , dann .

Bezeichnen wir diese Menge als . Dann heißt eine Extension von , wenn ein Fixpunkt von ist, dh. . Für jede Formel schreiben wir .

In Worten bedeutet die Operation : Die gegebene Faktenmenge muß in der Extension enthalten sein, und die Extension muß abgeschlossen sein gegenüber der Ableitbarkeitsoperation im klassischen Sinne (siehe Abschnitt 3.1) ebenso wie gegenüber den Ermangelungsregeln. Im allgemeinen wird eine Extension umfassender sein als die über der Faktenmenge gebildete Theorie, aber kleiner als die über der Fakten- und Regelmenge im klassischen Sinne gebildete Theorie, also insbesondere ohne Beachtung der Rechtfertigungen. Anders ausgedrückt heißt dies, daß die Menge der Modelle von größer ist als die von . Durch die Extensionsbildung wird also die Modellmenge eingeschränkt, eine Beobachtung, die wir uns im Hinblick auf die Semantik dieser Logik im Kopfe behalten sollten.

Eine intuitiv besser zu verstehende Charakterisierung von Extensionen ist die durch das folgende Theorem gegebene.

Sei eine Ermangelungstheorie, und sei eine Menge von Sätzen. Wir definieren und für

Dann ist eine Extension für genau dann, wenn gilt.

Die in diesem Theorem gegebene Charakterisierung der Extension einer Ermangelungstheorie ist von konstruktiverer Natur deswegen, weil die Extension in einer Reihe von Iterationsschritten gebildet wird. Die dem Problem innewohnende Zirkularität ist aber nicht verschwunden, sondern äußert sich in der Konsistenzprüfung der Rechtfertigungen bezüglich der gesamten (noch zu findenden) Extension bei jedem Iterationsschritt.

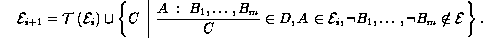
Wir können uns nun allerdings diese ``Konstruktion'' einer Extension anhand eines Übergangsgraphen verdeutlichen. Dieser hat die Form eines azyklischen, gerichteten Graphen, dessen Knoten Mengen von Formeln repräsentieren. Die (einzige) Wurzel des Graphen repräsentiert die deduktive Hülle der zugrundeliegende Faktenmenge . Jede Kante ist mit einer Ermangelungsregel markiert. Sie verbindet den Knoten zur Formelmenge mit einem Knoten zur Formelmenge genau dann, wenn die Voraussetzung in enthalten ist und die Rechtfertigungen mit konsistent sind, dh. wenn gilt. In diesem Sinne wird der Graph ``zu groß''. Seine Blätter können nämlich Extensionen repräsentieren, müssen es aber nicht.

Um nun zu überprüfen, ob eine ein Blatt markierende Formelmenge eine Extension darstellt, betrachten wir die Pfade von der Wurzel bis zu dem betreffenden Blatt. Unter ihnen muß im positiven Fall ein Pfad sein, so daß jede Rechtfertigung einer eine Kante des Pfades markierenden Ermangelungsregel konsistent bzgl. der Formelmenge des Blattes ist. Praktisch ist dieses Verfahren jedoch nur bei endlichen Graphen dieser Art durchführbar. Ein weiteres Verfahren zur Konstruktion von Extensionen findet sich in Abschnitt 3.4 von [Eth88].

Mit der Angabe der obigen Definition einer Extension ist natürlich nicht geklärt, ob es zu einer Ermangelungstheorie überhaupt eine Extension gibt. Bevor wir dieser Frage nachgehen, wollen wir aber den Begriff durch Beispiele veranschaulichen.

Wie immer betrachten wir das Eiscreme-Beispiel, zu dem wir die Ermangelungsregel

oben schon einmal angegeben haben. Zu ihr fügen wir jetzt die Faktenmenge hinzu, die nur aus besteht. ist hiermit offensichtlich konsistent, so daß abgeleitet werden kann. Damit sind jedoch schon alle deduktiven Möglichkeiten erschöpft, so daß wir die Extension erhalten.

Erweitern wir die Faktenmenge nun durch und die Regelmenge durch

so ergeben sich zwei verschiedene Extensionen, und . Wie wir sehen, ist die Situation wie bei früheren Ansätzen; erst durch irgendeine Form von Hierarchie läßt sich auch hier das gewünschte Resultat erzielen. Wir wollen uns nun aber wieder den grundlegenden theoretischen Fragestellungen, insbesondere der nach der semantischen Bedeutung und damit zusammenhängend nach der Existenz der Extension im allgemeinen Fall, zuwenden.