Pfade und Werte

Deﬁnition 12.2.1 (Merkmal-Pfad). Ein Pfad in einer Merkmalstruktur ist eine endliche Folge von Merkmalen, die in der Merkmalstruktur unmittelbar ineinander verschachtelt sind.

Beispiel 12.2.2 (Merkmalstruktur und alle nicht-leeren Pfade).
⌊ ⌊ [ ]⌋⌋
NUM sg
⌈SUBJ ⌈AGR PER 3 ⌉⌉
⟨SUBJ⟩ ⟨AGR⟩ ⟨NUM⟩
⟨SUBJ,AGR⟩ ⟨AGR,NUM⟩ ⟨AGR,PER⟩
⟨SUBJ,AGR,NUM⟩ ⟨SUBJ,AGR,PER⟩

Deﬁnition 12.2.3 (Vollständiger Pfad). Ein vollständiger Pfad einer Merkmalstruktur ist ein Merkmal-Pfad, der beim Wurzelknoten beginnt und bei einem atomaren Wert oder der leeren Merkmalstruktur endet.

Deﬁnition 12.2.4 (Wert eines Pfades). Der Wert eines Pfades ist der Wert, der am Ende des Pfades beginnt.

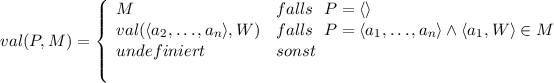
( ||| M falls P = ⟨⟩ { val(⟨a2,...,an⟩,W ) falls P = ⟨a1,...,an⟩ ∧⟨a1,W ⟩ ∈ M val(P, M ) = || undef iniert sonst |(

Beispiel 12.2.5 (Werte von Pfaden).

M= ⌊ ⌊ ⌋⌋
[NUM sg]
⌈SUBJ ⌈AGR ⌉⌉
PER 3

val(⟨SUBJ,AGR,NUM⟩,M) = sg
val(⟨SUBJ,AGR⟩,M) = [NUM sg ]

PER 3

Evaluation der Pfadfunktion
val(⟨SUBJ,AGR,NUM⟩, ⌊ ⌊ [ ]⌋⌋
⌈ ⌈ NUM sg ⌉⌉
SUBJ AGR PER 3

) = val(⟨AGR,NUM⟩, ⌊ [ ]⌋
⌈ NUM sg ⌉
AGR PER 3

) = val(⟨NUM⟩, [ ]
NUM sg
PER 3

) = val(⟨⟩, sg) = sg

schwamm   V * {
       (^ TENSE) = past
       (^ AGR PERS) = 3
       (^ AGR NUM) = sg
       |
       (^ TENSE) = past
       (^ AGR PERS) = 1
       (^ AGR NUM) = sg
      }.

12.2.1
Koreferenz

Koreferenz (structure sharing, reentrancy) in Merkmalstrukturen erzwingt die Identität von Werten bzw. von Teil-Merkmalstrukturen.

Beispiel 12.2.6 (Kongruenz von Subjekt und ﬁnitem Verb).
Im Satz «Hans schwamm.» sind die Wortformen «Hans» und «schwamm» für sich genommen morphologisch ambig.

Wir wissen: Welche Werte auch immer das ﬁnite Verb in Numerus und Person hat, das Subjekt muss dieselben haben.

Überall, wo es um den Abgleich von variabler linguistischer Information geht, ist Koreferenz das Mittel der Wahl. So etwas wie Anti-Koreferenz braucht es fast nie…

pict

Abbildung 12.3:

Koreferente Merkmalstruktur als Matritze

pict

Abbildung 12.4:

Koreferente Merkmalstruktur als gerichteter Graph

Koreferenz in XLE-Merkmalstrukturen
Die Koindizierung wird in XLE über die Identiﬁkationsnummer von Teilmerkmalstrukturen (3) und einer Pfadangabe (AGR) dargestellt.

pict

Abbildung 12.5:

Koreferente Merkmalstruktur als gerichteter Graph

Deﬁnition 12.2.7 (Merkmalstrukturen mit Koreferenz). Als Graph ist eine Merkmalstruktur mit Koreferenzen ein markierter gerichteter Baum, bei dem eine Bedingung aufgehoben ist:

Ein Knoten kann mehr als einen Vorgänger haben.

Bei der Matrix-Notation muss man genau bei einem Wert einen Index setzen und kann die koreferenten Werte dann damit koindizieren .

Koreferenz ist Gleichheitsrelation zwischen bestimmten Werten von Pfaden eine Merkmalstruktur M.

Beispiel 12.2.8 (Koreferenz von 2 Merkmal-Pfaden).

val(⟨SUBJ,AGR⟩,M) = val(⟨PRED,AGR⟩,M)

12.2 Pfade und Werte

12.2.1 Koreferenz

12.2
Pfade und Werte

12.2.1
Koreferenz