[ Weiter ] [ Seitenende ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]

12.1
 Merkmalstrukturen

12.1.1
 Motivation

Merkmalsanalysen 

Wissenschaftshistorische Motivation

Die Verwendung von (binären) Merkmalen in der modernen linguistischen Theorie geht zurück auf die Theorie der strukturalistischen Phonologie, wo die Analyse mit sogenannten «Distinktiven Merkmalen» zentral war.

Beispiel 12.1.1 (Merkmalsanalyse in der Phonologie).
Das Phonem /b/ = [+Verschlusslaut, +Bilabial, +Stimmhaft].

Beispiel 12.1.2 (Merkmalsanalyse in der Semantik nach Bierwisch).
Die Verwandschaftsbezeichnung «Cousin» [+Mensch, +verwandt, –direkt verwandt, +gleiche Generation, +männlich, –weiblich ].

Beispiel 12.1.3 (Merkmalsanalyse in der Syntax nach Chomsky).
Die Hauptwortarten Nomen, Verben, Adjektive und Präpositionen «A» [+Verbal,+Nominal] oder «P» [–Verbal,–Nominal].

Informationsorientierte Motivation 

Zur Bedeutung von Merkmalstrukturen

Merkmalstrukturen beschreiben Mengen von Objekten , welche bestimmte Bedingungen (constraints) erfüllen, die als Merkmal-Wert-Paare formuliert sind.

⌊ ⌋ | Wortart verb| |⌈ Numerus sg |⌉ Person 3

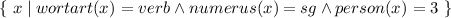
{ x | wortart(x) = verb∧ numerus (x) = sg ∧ person(x) = 3 }
∧ steht für logisches UND.

Unterspezifikation

Je weniger Merkmal-Wert-Paare in einer Merkmalstruktur spezifiziert sind,

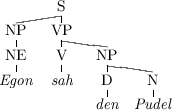
Merkmalstrukturen in der Syntax 
Wie kann die mehrdeutige Information aus dem Lexikon und der Syntaxanalyse widerspruchsfrei vereinigt werden zur Informationsstruktur des Satzes „Hans schwamm“?

Beispiel 12.1.4 (Merkmalstruktur des Satzes „Hans schwamm“).

⌊ ⌋ Subj [Lemma: ’Hans ’, Case:Nom, Pers:3, Num:Sg ] || Pred [Lemma: ’schwimmen ’, Tense:Past, Pers:3, Mood:Ind ]|| ⌈ ⌉ Clause Decl

Einfache Merkmalstrukturen 

Mengentheoretische Beschreibung

Eine einfache, d.h. nicht-rekursive Merkmalstruktur ist eine Abbildung M : A → V von einer endlichen Menge von Attributen A auf Werte V .

Beispiel 12.1.5 (Einfache linguistische Merkmalstrukturen).
[num pl] pers 1 M = {⟨num,pl⟩,⟨pers,1⟩}

Datenstrukturen in Programmiersprachen

Dies entspricht Hashes (PERL), Dictionaries (PYTHON), Records (PASCAL), Listen von Merkmal-Wert-Paaren (PROLOG, LISP) oder Eigenschaften von Objekten (JAVA).

12.1.2
 Rekursiv

Beispiel: Gegenseitig rekursiv definierte Mengen 

Gerade Zahlen

Ungerade Zahlen

Sätze und NP

Da Sätze Nominalphrasen enthalten und Nominalphrasen wiederum (Relativ-)Sätze enthalten können, müssen diese Kategorien auch gegenseitig rekursiv definiert werden.

Merkmalstrukturen gegenseitig rekursiv definiert 

Definition 12.1.6 (Attribut-Wert-Struktur, attribute value matrix (AVM)). Die Menge der Merkmalstrukturen aus einer Menge A von Merkmalen (Attributen) und V von atomaren Werten lässt sich rekursiv angeben.

Merkmalstrukturen

Werte

Beispiel: Rekursive Konstruktion einer Merkmalstruktur M

Sei V = {sg,pl,1,2,3} und A = {AGR,NUM,PER}

Schritt

als Menge

in Matrix-Notation

1

M1 = ∅

M1 =[]

2

M2 = M1 ∪{⟨PER,3⟩}

M2 =[ ] PER 3

3

M3 = M2 ∪{⟨NUM,sg⟩}

M 3 =[ ] NUM sg PER 3

4

M = M1 ∪{⟨AGR,M3⟩}

M =⌊ ⌋ [NUM sg] ⌈AGR ⌉ PER 3

12.1.3
 Als Graphen

Gerichtete Graphen 

Definition 12.1.7 (directed graph, digraph). Ein gerichteter Graph G = ⟨N,E⟩ besteht aus einer endlichen, nicht-leeren Menge N von Knoten (nodes) und einer Menge E von Kanten (edges): E ⊆ N × N.

pict
G = ⟨{a,b,c,d},
{⟨a,b⟩,⟨b,c⟩,⟨b,d⟩,
⟨c,a⟩,⟨d,a⟩,⟨d,c⟩}⟩

Definition 12.1.8 (Verbindungen und Pfade). Ein Pfad ist eine endliche Folge von Knoten, welche paarweise durch Kanten verbunden sind. Z.B. ⟨d,c,a,b⟩.

Die Knoten n1 und n2 sind verbunden im Graphen G = ⟨N,E⟩, gdw. ⟨n1,n2⟩∈ E.

n1 heisst Vorgänger von n2. n2 heisst Nachfolger von n1.

Zyklen 

Definition 12.1.9 (Einfacher Pfad). Ein einfacher Pfad ist ein Pfad, der einen Knoten höchstens einmal enthält.

Definition 12.1.10 (Zyklus). Ein Zyklus ist ein einfacher Pfad, an dessen Ende nochmals sein Anfangselement angefügt wird.

Zyklen der Form ⟨n,n⟩ heissen auch Schlaufen (loop).

Definitionsabhängig werden Schlaufen manchmal nicht als Zyklen aufgefasst.

Definition 12.1.11 (Zyklenfrei). Ein Graph, der keine Zyklen enthält, heisst zyklenfrei .

Bäume 

Definition 12.1.12 (Gerichteter Baum). Ein Baum ist ein zyklenfreier, gerichteter Graph mit den Eigenschaften:

Definition 12.1.13 (Matrilineare Sprechweisen). Zwei Knoten sind Schwestern (Geschwister), wenn sie denselben Vorgänger (Mutter ) haben.

S | NP VP| NE V| NP Egon sah D N | | den Pudel

Markierte gerichtete Bäume 

Definition 12.1.14 (markierter gerichteter Baum). Ein markierter gerichteter Baum ist ein gerichteter Baum T = ⟨N,E⟩. Er besitzt eine Markierungsfunktion für Kanten mE : E → A, welche jeder Kante eine Markierung aus A zuordnet. Sowie eine Markierungsfunktion für Knoten mN : N → B, welche jedem Knoten eine Markierung aus B zuordnet.

Definition 12.1.15 (Blatt). Die Blätter eines Baumes sind alle seine Knoten ohne Nachfolger.

Definition 12.1.16 (Innere Knoten). Die inneren Knoten eines Baumes sind alle Knoten mit mindestens einem Nachfolger.

Merkmalstruktur als markierter gerichteter Baum 

Beispiel 12.1.17.
T = ⟨N,E⟩
N = {n1,n2,n3,n4}
E = {⟨n1,n2⟩,⟨n2,n3⟩,⟨n2,n4⟩}
mE = {⟨⟨n1,n2⟩,AGR⟩,⟨⟨n2,n3⟩,PERS⟩,⟨⟨n2,n4⟩,NUM⟩} mN = {⟨n1,′′⟩,⟨n2,′′⟩,⟨n3,3⟩,⟨n4,sg⟩}

pict

Abbildung 12.1: Merkmalstruktur als gerichteter Baum

pict

Abbildung 12.2: Kästchennotation

Merkmalstrukturen und Bäume 

Definition 12.1.18 (Baum einer koreferenzfreien Merkmalstruktur). Ein markierter gerichteter Baum T stellt eine Merkmalstruktur M dar, gdw. er folgende Eigenschaften erfüllt:

[ Weiter ] [ Seitenbeginn ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]