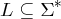
[ Seitenende ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]

4.1.  Formale Sprachen

4.1.1.  Zeichen und Zeichenketten

4.1.2 Formale Sprachen
4.2 EA
4.2.1 DEA
4.2.2 NEA
4.2.3 ε-NEA
4.3 Reguläre Sprachen
4.3.1 Konkatenation
4.3.2 Stern
4.3.3 Rekursive Definition
4.4 RA
4.4.1 Symbole
4.4.2 Operatoren
4.5 Vertiefung

Das Alphabet (Sigma), Zeichen und Zeichenketten

Definition 4.1.1. Ein Alphabet ist eine endliche Menge von Zeichen (atomare Symbole). Es wird mit Σ (Sigma) notiert.

Definition 4.1.2. Eine Zeichenkette (Wort, string) von n Zeichen aus Σ ist eine endliche Folge der Länge n über Σ.

Die leere Zeichenkette (leeres Wort) ist die Folge von 0 Zeichen. Sie wird mit ε (Epsilon) notiert und hat die Länge 0.

Hinweis zur Notation

Eine Zeichenkette wird typischerweise durch Nebeneinanderschreiben (Juxtaposition) der Zeichen von links nach rechts notiert.

Sei Σ = {a,b}, dann sind etwa ε, a, bb oder ababbba Wörter über Σ.

4.1.2.  Formale Sprachen als Menge von Zeichenketten

Stern von Sigma und formale Sprachen

Definition 4.1.3. Der Stern von Sigma ist die Menge aller Wörter über einem Alphabet Σ. Der Stern wird als Postfix-Operator Σ∗ (sprich «Sigma Stern») notiert.

Definition 4.1.4.

Eine formale Sprache L über Σ ist eine Teilmenge des Sterns von Sigma.

L ⊆ Σ∗

Beispiel 4.1.5. Sei Σ = {a}, dann ist Σ∗ = {ε,a,aa,aaa,…}. Die Mengen L1 = {ε,a} oder L2 = {aa,aaaa,aaaaaa} sind formale Sprachen, da sie (echte) Teilmengen von Σ∗ sind.

Leere Sprachen vs. leere Zeichenkette

Hinweise

Fragen