Endliche Automaten

[ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]

4.2. Endliche Automaten

4.2.1. Deterministische endliche Automaten

4.2.2 NEA
4.2.3 ε-NEA
4.3 Reguläre Sprachen
4.3.1 Konkatenation
4.3.2 Stern
4.3.3 Rekursive Deﬁnition
4.4 RA
4.4.1 Symbole
4.4.2 Operatoren
4.5 Vertiefung

Deterministische Endliche Automaten (DEA)

Idee des akzeptierenden deterministischen endlichen Automaten

Ein endlicher Automat ist eine (abstrakte) Maschine zur zeichenweisen Erkennung von Wörtern einer regulären Sprache. Sie ist nach jedem Verarbeitungsschritt in genau einem Zustand. Bei jedem Schritt wird ein Zeichen gelesen und aufgrund des aktuellen Zustands und dem Lesezeichen in einen Nachfolgezustand gewechselt. Wenn kein Zeichen mehr zu lesen ist und die Maschine in einem Endzustand ist, gilt die gelesene Zeichenkette als akzeptiert. Beim Einlesen des ersten Zeichens einer Zeichenkette ist der Automat immer im sogenannten Startzustand.

Deﬁnition 4.2.1 (DEA, ﬁnite state automaton).

Ein deterministischer endlicher Automat A = 〈Φ,Σ,δ,S,F〉 besteht aus

einer endlichen Menge Zustände Φ
einem endlichen Eingabealphabet Σ
einer Zustandsübergangsfunktion δ : Φ × Σ → Φ
einem Startzustand S ∈ Φ
einer Menge von Endzuständen F ⊆ Φ

Hinweis

Die Übergangsfunktion δ bestimmt den Folgezustand, der ausgehend vom aktuellen Zustand beim Lesen eines einzelnen Zeichens erreicht wird.

Zustandübergangsdiagramm
Es stellt einen EA anschaulich als gerichteten Graphen dar.

Beispiel 4.2.2.

A = 〈{0,1},{a,b},δ,0,{1}〉 mit δ = {〈〈0,a〉,1〉,〈〈0,b〉,1〉,〈〈1,a〉,1〉,〈〈1,b〉,1〉}

pict

Abbildung 4.1:

Zustandsübergangsdiagramm

Jeder Zustand ist ein Knoten.
Der Startzustand ist mit einem freien Pfeil oder auch nur mit der Beschriftung 0 (Null) bzw. S (Start) markiert.
Endzustände sind doppelt umrahmt.
Jeder Zustandsübergang ist eine gerichtete Kante vom aktuellen Zustand zum Folgezustand mit dem Zeichen als Kantenlabel.
Alternative Zeichen werden oft mit einem Pfeil kondensiert dargestellt.

Sprache eines DEA

Deﬁnition 4.2.3 (Zustandsübergangsfunktion für Zeichenketten).

Die auf Zeichenketten erweiterte Übergangsfunktion δ^∗ : Φ × Σ^∗→ Φ bestimmt den Zustand nach dem vollständigen Lesen eines Wortes.

Für alle T ∈ Φ,ω ∈ Σ^∗,x ∈ Σ eines DEA A = 〈Φ,Σ,δ,S,F〉

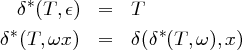
∗ δ (T, ε) = T δ∗(T,ωx ) = δ(δ∗(T, ω),x)

Deﬁnition 4.2.4.

Die Sprache L(A) eines DEA A = 〈Φ,Σ,δ,S,F〉 ist die Menge aller Zeichenketten, für die δ^∗ ausgehend vom Startzustand einen Endzustand ergibt.

L = {ω ∈ Σ∗ | δ∗(S,ω) ∈ F} A

Beispiel-Berechnung für δ^∗ aus Beispiel ??

δ^∗(0,aba)
= δ(δ^∗(0,ab),a)
= δ(δ(δ^∗(0,a),b),a)
= δ(δ(δ(δ^∗(0,ε),a),b),a)
= δ(δ(δ(0,a),b),a)
= δ(δ(1,b),a)
= δ(1,a)
= 1

Beispiel-Evaluation
Siehe Abb. 4.2 auf Seite 125.

Abbildung 4.2:

Beispielevaluation der erweiterten Übergangsfunktion für DEA

Partielle Zustandübergangsdiagramme
Die Deﬁnition von δ als totale Funktion verlangt für alle Zustände und Zeichen aus Σ eine Kante. In der Linguistik zeigt man oft nur Knoten und Kanten, die für das Akzeptieren einer Zeichenkette relevant sind.

Beispiel 4.2.5 (Partieller und vollständiger Automat).

pict

Fehlerzustand (error state) und Fehlerübergänge

Um ein partielles Übergangsdiagramm zu vervollständigen, füge einen Zustand E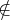F dazu, und mache ihn zum Endknoten aller nicht-bestehenden Kanten.

EA im XFST-Prolog-Format

Beispiel 4.2.6 (Direktes Einlesen von EA im PROLOG-Format).

xfst[0]: read prolog
Type one or more networks in prolog format.
Use ^D to terminate input.
arc(ex2,0,1,"a").
arc(ex2,1,2,"b").
final(ex2,2).

pict

Kantenrepräsentation: arc(ID, VON, NACH, ZEICHEN)
0 ist Startzustand.
Endzustände: final(ID, ZUSTAND)
Schreiben von EA Prolog-Format: write prolog > Dateiname
Einlesen aus Datei: read prolog < Dateiname

Textuelle Ausgabe von EA

Beispiel 4.2.7 (Anzeige von Informationen zum obersten EA auf dem Stack).

xfst[1]: print net
Sigma: a b
Size: 2
Net: ex2
Flags: epsilon_free
Arity: 1
s0: a -> s1.
s1: b -> fs2.
fs2: (no arcs)

Sigma : Auﬂistung aller Zeichen des Alphabets
Size : Anzahl der Kantenbeschriftungen
Net : Name des EA
Flags : Wichtige Eigenschaften bzgl. ε, Sprachgrösse, EA-Typ usw.
Arity : 1 = EA, 2 = Transduktor
s0: Startzustand; für n > 0
fsn : Endzustand, sn : Kein Endzustand
s1: b -> fs2.: Vom Zustand s1 geht eine mit b beschriftete Kante zum Folgezustand fs2.

Wichtige in xfst berechenbare Eigenschaften von EA
Tests bezüglich endlicher Automaten auf dem Stack

Ist eine Zeichenkette w Element der Sprache eines EA?
xfst[1]: apply up w w ∈ L(EA)
Ist die Sprache von EA die leere Sprache ?
xfst[1]: test null L(EA) = ∅
Ist die Sprache von EA die universale Sprache ?
xfst[1]: test lower-universal L(EA) = Σ^∗

Wichtige in xfst berechenbare Beziehungen von EA

EA₂ =

EA₁ =

Abbildung 4.3:

EA₂ auf EA₁ auf dem Stack

Tests bezüglich endlicher Automaten auf dem Stack (EA₂ auf EA₁)

Besitzen EA₁ und EA₂ die gleiche Sprache ?
xfst[2]: test equivalent L(EA₁) = L(EA₂)
Ist die Sprache von EA₁ Teilmenge der Sprache von EA₂?
xfst[2]: test sublanguage L(EA₁) ⊆ L(EA₂)

Anstelle von apply up kann man auch apply down sagen. Statt test lower-universal auch upper-universal. Diese Sprechweisen hängen mit den Transduktoren zusammen, welche eine “obere” und “untere” Sprache haben. Bei den endlichen Automaten sind aber beide Sprachen gleich.

4.2.2. Nicht-deterministische endliche Automaten

Nicht-deterministischer endlicher Automat (NEA)

Idee des akzeptierenden nicht-deterministischen endlichen Automaten

Im Gegensatz zum DEA kann ein NEA nach jedem Verarbeitungsschritt in mehr als einem Zustand sein. Bei jedem Schritt wird ebenfalls ein Zeichen gelesen und aufgrund der möglichen aktuellen Zustände und dem Lesezeichen in die zulässigen Nachfolgezustände gewechselt.

Beispiel-Evaluation
Siehe Abb. 4.2.2 auf Seite 134.

Abbildung 4.4:

Beispielevaluation der erweiterten Übergangsfunktion für NEA

Deﬁnition 4.2.8 (NEA, non-deterministic ﬁnite state automaton).

Ein nicht-deterministischer endlicher Automat A = 〈Φ,Σ,δ,S,F〉 unterscheidet sich von einem DEA nur in der Übergangsfunktion. Vom aktuellen Zustand kann man mit einem Zeichen zu beliebig vielen Folgezuständen übergehen.

δ : Φ × Σ → ℘(Φ)

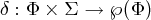
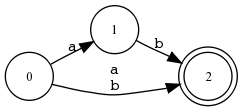
Beispiel 4.2.9 (Tabellendarstellung und Zustandsdiagramm).

δ	a	b

s0	{s1,fs2}	{fs2}
s1	∅	{fs2}
fs2	∅	∅

pict

Sprache von NEA

Deﬁnition 4.2.10 (Zustandsübergangsfunktion für Zeichenketten).

Die auf Zeichenketten erweiterte Übergangsfunktion δ^∗ : Φ × Σ^∗→ ℘(Φ) bestimmt die Menge der erreichbaren Zustände nach dem vollständigen Lesen einer Zeichenkette.

Für alle T ∈ Φ,ω ∈ Σ^∗,x ∈ Σ eines NEA A = 〈Φ,Σ,δ,S,F〉

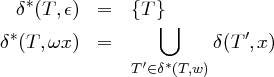
δ∗(T,ε) = {T } ∗ ⋃ ′ δ (T,ωx ) = δ(T ,x) T′∈δ∗(T,w)

Deﬁnition 4.2.11.

Die Sprache L(A) eines NEA A = 〈Φ,Σ,δ,S,F〉 ist die Menge aller Zeichenketten, für die δ^∗ ausgehend vom Startzustand mindestens einen Endzustand enthält.

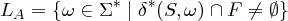
∗ ∗ LA = {ω ∈ Σ | δ (S,ω )∩ F ⁄= ∅}

Beispiel-Berechnung für δ^∗

$δ∗(0,ab)$
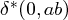
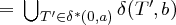
$⋃ = T′∈ δ∗(0,a)δ(T′,b)$
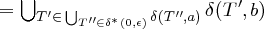
$⋃ = T ′∈⋃ ′′ ∗ δ(T′′,a)δ(T ′,b) T ∈δ(0,ε)$
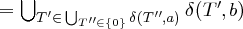
$⋃ = T ′∈⋃ ′′ δ(T′′,a)δ(T′,b) T ∈{0}$
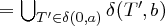
$⋃ = T ′∈δ(0,a)δ(T′,b)$
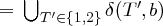
$⋃ = T′∈ {1,2} δ(T ′,b)$
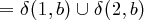
$= δ(1,b) ∪δ(2,b)$
$= {2}∪ ∅$
$= {2}$

4.2.3. Nicht-deterministische endliche Automaten mit ε

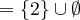
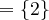
Idee des akzeptierenden nicht-deterministischen endlichen Automaten mit ε

Bei jedem Schritt wird wie beim NEA ein Zeichen gelesen und aufgrund der möglichen aktuellen Zustände und dem Lesezeichen in die zulässigen Nachfolgezustände gewechselt.

Die aktuellen Zustände umfassen aber immer auch alle Zustände, welche durch beliebig viele ε-Übergange verbunden sind.

Bei einem ε-Übergang wird kein Zeichen gelesen.

Deﬁnition 4.2.12 (ε-NEA, non-deterministic ﬁnite state automaton).

Ein nicht-deterministischer endlicher Automat mit ε-Übergängen A = 〈Φ,Σ,δ,S,F〉 unterscheidet sich von einem NEA nur in der Übergangsfunktion.

δ : Φ × Σ ∪{ε}→ ℘(Φ)

Die Bestimmung der Übergangsfunktion δ^∗ auf Zeichenketten setzt auf der reﬂexiven und transitiven Hülle der ε-Übergänge auf.

Deﬁnition 4.2.13.

Die ε-Hülle δ_ε^∗ : Φ → ℘(Φ) eines ε-NEA für einen Zustand T ∈ Φ ist rekursiv deﬁniert durch:

T ∈ δ_ε^∗(T)
Falls T₁ ∈ δ_ε^∗(T) und T₂ ∈ δ(T₁,ε), dann T₂ ∈ δ_ε^∗(T).

Sprache von NEA mit ε

Deﬁnition 4.2.14 (Zustandsübergangsfunktion für Zeichenketten). Die auf Zeichenketten erweiterte Übergangsfunktion δ^∗ : Φ × (Σ ∪{ε})^∗→ ℘(Φ) bestimmt die Menge der erreichbaren Zustände nach dem vollständigen Lesen einer Zeichenkette.

Für alle T ∈ Φ,w ∈ Σ^∗,x ∈ Σ eines ε-NEA A = 〈Φ,Σ,δ,S,F〉

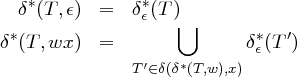
∗ ∗ δ (T,ε) = δε(T)⋃ δ∗(T,wx ) = δ∗ε(T′) T′∈δ(δ∗(T,w),x)

Die Sprache eines ε-NEA ist gleich deﬁniert wie bei NEA ohne ε.

QUIZ Leichtes QUIZ zu endlichen Automaten

Äquivalenz der Sprachen von DEA, NEA und ε-NEA

Entfernung von ε-Übergängen

Für jeden ε-NEA lässt sich ein NEA (ohne ε) konstruieren, der die gleiche Sprache akzeptiert.
xfst[1]: epsilon-remove net

Entfernung von Nicht-Determinismus

Für jeden NEA lässt sich ein DEA konstruieren, der die gleiche Sprache akzeptiert.
xfst[1]: determinize net

Entfernung unnötiger Zustände

Für jeden DEA lässt sich ein DEA mit minimaler Anzahl Zustände konstruieren, der die gleiche Sprache akzeptiert.
xfst[1]: minimize net

Der Befehl minimize net beinhaltet die Entfernung von ε-Übergängen und die Determinisierung. D.h. ein minimisierter EA ist immer deterministisch und ohne ε-Übergängen.

Beispiel für äquivalente EA
Siehe Abb. 82 auf Seite 146.



ε-NEA	nach epsilon-remove


nach determinize	nach minimize

Abbildung 4.5:

Eﬀekt der 3 EA-Transformationen