Reguläre Sprachen

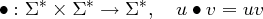
[ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]

4.3. Reguläre Sprachen

4.3.1. Konkatenation

4.3.3 Rekursive Deﬁnition
4.4 RA
4.4.1 Symbole
4.4.2 Operatoren
4.5 Vertiefung

Konkatenation von Zeichenketten und Sprachen

Deﬁnition 4.3.1. Die Konkatenation von Zeichenketten ist eine zweistellige Funktion, welche ihre Argumente zu einem Wort verkettet. Für alle u,v ∈ Σ^∗:

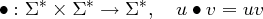
∙ : Σ∗ × Σ∗ → Σ ∗, u∙ v = uv

Deﬁnition 4.3.2. Die Konkatenation von Sprachen erweitert Verkettung auf Mengen von Zeichenketten. Für alle M,N ⊆ Σ^∗:

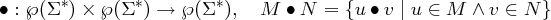
∙ : ℘(Σ∗)× ℘ (Σ∗) → ℘(Σ ∗), M ∙ N = {u ∙v | u ∈ M ∧ v ∈ N }

Eigenschaften der Konkatenation

Zeichenketten

Die Konkatenation ist assoziativ und hat ε als neutrales Element . Für alle u,v,w ∈ Σ^∗:

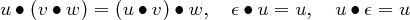
u ∙(v ∙w ) = (u ∙v) ∙w, ε∙ u = u, u∙ ε = u

Sprachen

Die Konkatenation ist assoziativ und hat {ε} als neutrales Element . Für alle M,N,P ⊂ Σ^∗:

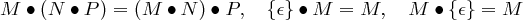
M ∙(N ∙P ) = (M ∙N ) ∙P, { ε} ∙M = M, M ∙ {ε} = M

Klammerung

Die Assoziativität der Konkatenation macht Klammern optional.

4.3.2. Stern

Stern einer Sprache (Kleene star)

Deﬁnition 4.3.3. Die n-fache Konkatenation einer Sprache L mit sich selbst in der Potenznotation sei rekursiv deﬁniert. Für n ≥ 1,n ∈ ℕ:

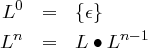
0 L = {ε} Ln = L ∙Ln −1

Deﬁnition 4.3.4. Der Stern einer Sprache (Kleene-Hülle) ist Vereinigung ihrer Konkatenationen.

∗ ∗ ∗ ∗ 0 1 2 3 ⋃ n : ℘ (Σ ) → ℘(Σ ), L = L ∪ L ∪ L ∪L ∪ ...= L n≥0

Plus einer Sprache

Beispiel 4.3.5. Sei M = {ab,c}über Σ = {a,b,c}. Welche Zeichenketten enthält M^∗?

Hinweis

Formale Sprachen sind Mengen und somit können alle Mengenoperationen wie Schnitt (M ∩ N), Vereinigung (M ∪ N), Mengendiﬀerenz (M ∖ N) mit ihnen verwendet werden.

Deﬁnition 4.3.6. Das Plus einer Sprache (positive Kleene Hülle) ist

+ ∗ ∗ + ∗ : ℘(Σ ) → ℘ (Σ ), L = L ∖{ε}

4.3.3. Rekursive Deﬁnition

Reguläre Sprachen

Deﬁnition 4.3.7. Eine Sprache über Σ = {a₁,a₂,...,a_n} heisst regulär , wenn sie durch folgende reguläre Mengenausdrücke beschrieben werden kann:

Die leere Menge ∅ ist regulär.
Die Menge {ε} ist regulär.
Die Mengen {a_i} (1 ≤ i ≤ n) sind regulär.
Wenn L₁ und L₂ regulär sind, dann auch (L₁ ∪ L₂).
Wenn L₁ und L₂ regulär sind, dann auch (L₁ ∙ L₂).
Ist L regulär, dann auch L^∗.

Diese 6 Bildungsregeln reichen aus, um alle regulären Sprachen zu beschreiben. Meistens werden für die Kürze der Notation noch weitere Konstrukte deﬁniert, welche sich aber immer auf obige 6 Bildungsregeln zurückführen lassen müssen.

Abschlusseigenschaften regulärer Sprachen

Deﬁnition 4.3.8. Eine Menge M heisst abgeschlossen (closed under) bezüglich einer Operation oder Funktion, wenn das Ergebnis der Operation mit Elementen aus M immer ein Element aus M ist.

Abschlusseigenschaften regulärer Sprachen

Über der Menge der regulären Sprachen sind die Operationen L₁ ∙ L₂, L^∗ und L ∪ L₂ per Deﬁnition abgeschlossen.
Der Abschluss bezüglich der Operationen L₁ ∩ L₂, L₁ ∖ L₂, L⁺ und Komplementmenge L lässt sich beweisen.

Reguläre Sprachen und EA
Die Menge der regulären Sprachen ist gleich der Menge der von EA akzeptierten Sprachen.

QUIZ Leichtes QUIZ zu Zeichenketten, Sprachen und Konkatenation