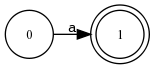
Beispiel 4.4.2 (xfst und Zustandsdiagramm).
read regex a ;
[ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Reguläre Ausdrücke (RA) in XFST
Normales Zeichensymbol
Jedes der folgenden Symbole x bezeichnet als regulärer Ausdruck (RA) die Sprache {x}:
%-geschütztes Zeichensymbol (%-escape)
Das Zeichen % gefolgt von einem der folgenden Symbole x
0 ? + * | . , : ; - / % ~ ( ) [ ] { } " \
bezeichnet als RA die Sprache {x}.
Hinweise
Zitiertes Zeichensymbol
Jedes Zeichen x zwischen doppelten Hochkommata ausser
\, " und getippter Zeilenwechsel
bezeichnet als RA die Sprache {x}.
Hinweis
Zwischen Hochkommata verlieren alle Zeichen ihre Sonderbedeutung.
Backslash-Notation zwischen doppelten Hochkommata
Backslash-Notation für nicht-druckbare Zeichen
und numerische Zeichenkodes
sind zwischen doppelten Hochkommata möglich.
Hinweise
Symbole aus mehreren Zeichen (multicharacter symbols)
Jede Folge von normalen Zeichen oder %-geschützten Zeichen ist ein Mehrzeichensymbol x, das als RA
die Sprache {x} bezeichnet.
Hinweis
Mehrzeichensymbole werden von einem endlichen Automaten in einem einzigen Zustandübergang konsumiert.
Zitierte Mehrzeichensymbole
Auch Mehrzeichensymbole lassen sich mit doppelten Hochkommata zitieren. Es gelten die gleichen
Regeln wie bei den Einzelzeichensymbole. In zitierten Symbolen verliert % seine Rolle als
Escape-Zeichen.
Guter Programmierstil
Epsilon-Symbol
Das Ziffern-Zeichen 0 ist ein Spezial-Symbol, das als RA die Sprache {ε} bezeichnet.
Hinweis
Any-Symbol
Das Zeichen ? ist ein Spezial-Symbol, das als RA die Sprache aller Zeichenketten der Länge 1
bezeichnet.
Hinweis
Reguläre Operatorenausdrücke in xfst
Wenn die beiden RA A und B die Sprachen A bzw. B bezeichnen, dann bezeichnet der
RA
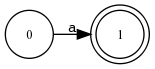
Beispiel 4.4.9 (Präzedenz von Operatoren). Welcher der beiden RA entspricht dem Zustandsdiagramm?
read regex a | b & c ;
read regex a | [ b & c ] ; |
Kurznotation für Konkatenation
Für beliebige druckbare Zeichen x ausser ’}’ steht der RA {x1 … xn} für [x1 … xn], d.h. die
Konkatenation {x1}∙… ∙{xn}.
Beispiel 4.4.10 (xfst und Zustandsdiagramm).
read regex {clear}|{clever}
|{ear}|{ever} |{fat}|{father}; |
![]()
Hinweis
Endliche Automaten speichern Lexika kompakter als Suchbäume (Buchstabenbäume, Trie), weil für die Wörter nicht bloss die gemeinsamen Präfixe, sondern auch die gemeinsamen Suffixe nur einmal repräsentiert sind.
Operatoren für Komplemente
Wenn der RA A die Sprache A über Σ bezeichnet, dann bezeichnet der RA
Universale Sprache, Komplement und Subtraktion
Die Sprache Σ∗ notiert sich in xfst als [ ?* ] und heisst universale Sprache . Für das Sprach-Komplement von A gilt die folgende Äquivalenz
[ ˜ A ] = [?* - A ].
Was gilt für das Komplement des Alphabets?
Das UNKNOWN-Symbol in endlichen Automaten
Das ANY-Symbol ? steht als RA für die Sprache aller Zeichenketten der Länge 1.
Beispiel 4.4.11 (?* - [a b] , d.h. ˜ [a b]).
xfst[0]: read regex [ ~ [ a b ] ] ;
280 bytes. 4 states, 12 arcs,Circular. xfst[1]: print net Sigma: ? a b fs0: ? -> fs1, a -> fs2, b -> fs1. fs1: ? -> fs1, a -> fs1, b -> fs1. fs2: ? -> fs1, a -> fs1, b -> s3. s3: ? -> fs1, a -> fs1, b -> fs1. |
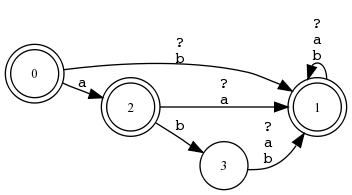
Im regulären Ausdruck ?*, der die universale Sprache bezeichnet, bedeutet das Fragezeichen nicht dasselbe wie als Kantenbeschriftung. Die Verwendung des gleichen Zeichens für unterschiedliche Zwecke mag verwirren. Die Funktion als Kantenbeschriftung und als regulärer Ausdruck lässt sich aber immer leicht unterscheiden.
Definition 4.4.12 (UNKNOWN-Symbol). Das UNKNOWN-Symbol ? an den Kantenübergängen von EA steht für diejenigen Symbole des Eingabealphabets, welche nicht explizit im xfst-Sigma aufgeführt sind, d.h. noch unbekannt sind.
Wozu kann es nützlich sein, das Alphabet nicht vollständig aufzählen zu müssen?
Operatoren für Enthalten-Sein
Wenn der RA A die Sprache A über Σ bezeichnet, dann bezeichnet der RA
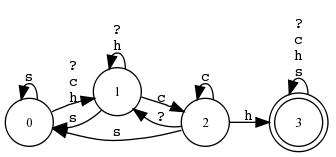
Die Sprache aller Wörter, welche mindestens ein ’ch’ enthalten, dem ein anderer Buchstabe als ’s’ vorangeht. von [$ [ \s c h] ]
Operator für Kontext-Beschränkung (restriction)
Wenn die RA A, L, R die Sprachen A, L bzw. R über Σ bezeichnen, dann bezeichnet [ A => L _ R ]
die Sprache
~ [ [~ [?* L] A ?*] | [?* A ~ [R ?*] ] ]
|
Die Sprache des Restriktions-Ausdrucks schränkt nur diejenigen Zeichenketten ein, welche als Teilzeichenkette ein Wort a aus A enthalten. Jedem a muss eine Zeichenkette aus L vorangehen und eine Zeichenkette aus R nachfolgen.
Beispiel 4.4.14. Die Sprache von [ a => b _ c ] umfasst das Wort back-to-back, aber nicht das Wort cab oder pack.
Wortende verankern in der Kontext-Beschränkung
Die Spezialmarkierung für Wortende
Die Kontexte in [ A => L _ R ] sind gegen Aussen implizit mit der universalen Sprache konkateniert: [ A => ?* L _ R ?*]. Die Spezialmarkierung .#. bedeutet in den Kontexten Verankerung am Wortende und verhindert so die implizite Verkettung. Im EA ist .#. nicht vorhanden, es kann aber wie ein Symbol in die RA eingefügt werden.
Beziehung zwischen RA, DEA und formalen Sprachen
Zu jedem regulären Ausdruck RA existiert mindestens ein EA, der die vom RA bezeichnete reguläre
Sprache akzeptiert.
|
|
Hinweise zur Definition der Operatoren Im Aufsatz [COHEN-SYGAL und WINTNER 2005] werden xfst-Konstrukte in den Formalismus der freiverfügbaren Prolog-basierten FSA-Tools von G. van Noord übersetzt.