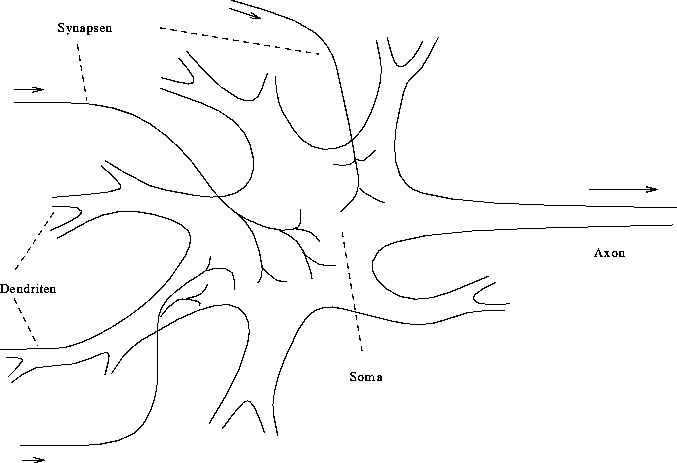
Abbildung 2.29: Schematische Darstellung eines Neurons






In der Neurologie hat man schon vor mehr als hundert Jahren Modelle entworfen, die die Funktionsweise des menschlichen Nervensystems zu erklären versuchen. Erst mit der genaueren Kenntnis der Struktur und des Aufbaus des Nervensystems [Ecc75] haben diese Modelle ab der Mitte dieses Jahrhunderts präzisere Formen angenommen. Abbildung 2.29 zeigt ein Neuron, den Grundbaustein des Nervensystems. Es besteht aus dem Hauptkörper, genannt das Soma, und aus kurzen Fortsätzen, den Dendriten, sowie aus dem sogenannten Axon mit mehreren Terminalen. Diese Terminale sind über Synapsen mit Dendriten anderer Neurone verbunden. Signale, die ein Neuron an seinen Dendriten empfängt, werden an das Soma weitergeleitet. An der Stelle, an der das Axon aus dem Hauptkörper heraustritt, baut sich das sogenannte Aktionspotential auf. Ist dieses Potential groß genug, dann wird es durch das Axon an die Terminale propagiert und über Synapsen an andere Neuronen weitergeleitet. Dabei unterscheidet man zwei Arten von Synapsen. Erregende (engl. excitatory) Synapsen verstärken das Aktionspotential des postsynaptischen Neurons, während es von hemmenden (engl. inhibitory) Synapsen vermindert wird.

Abbildung 2.29: Schematische Darstellung eines Neurons
Gleichzeitig mit der Modellentwicklung hat man damit begonnen, derartige Modelle mit den damals neuen technischen Möglichkeiten des Computereinsatzes experimentell zu erproben. Bevor wir uns den verschiedenen Modellen zuwenden, wollen wir zunächst einen gemeinsamen konzeptuellen Rahmen festlegen [FB82, RMt86]. Man kann in allen von ihnen die folgenden Aspekte unterscheiden, die dann im Verlauf dieses Abschnitts weiter besprochen werden.
Die Modelle arbeiten synchron oder asynchron. In einem synchronen Modell berechnen die Einheiten ihr Potential und
ihre Ausgabe zu jedem Takt einer globalen Uhr. Dies wird angezeigt, indem die
bestimmenden Größen wie Potential oder Eingabevektor mit dem Parameter
![]() versehen werden. In einem asynchronen Modell hingegen wird in jedem
Zeitschritt eine Einheit ausgewählt, die dann ihr Potential und ihre
Ausgabe neu bestimmt.
versehen werden. In einem asynchronen Modell hingegen wird in jedem
Zeitschritt eine Einheit ausgewählt, die dann ihr Potential und ihre
Ausgabe neu bestimmt.
Eines der ersten künstlichen neuronalen Modelle wurde von W. S. McCulloch und W. Pitts entwickelt [MP43]. Sie zeigten, daß ein synchrones Netzwerk, bestehend aus einfachen logischen Schwellenwerteinheiten, jede endliche logische Aussage realisieren kann (siehe Aufgabe 6.1.30). Das heißt unter anderem, daß ein solches Netzwerk auch alle Fähigkeiten eines klassischen Rechners aufweist.
In diesem Netzmodell summiert eine logische
Schwellenwerteinheit
in jedem Zeitschritt ihre gewichteten Eingaben auf und vergleicht die so
erhaltene Summe mit einem vordefinierten Schwellenwert ![]() , dh.
Aktivierungs- und Ausgabefunktion sind definiert als
, dh.
Aktivierungs- und Ausgabefunktion sind definiert als
![]()
Eine McCulloch-Pitts-Einheit ``feuert'' also, wenn die Summe der gewichteten Eingaben den Schwellenwert übersteigt. Schon an diesem Modell werden drei Grundprinzipien künstlicher neuronaler Netze deutlich.
Die Aufgabe, ein lernfähiges System zu entwickeln, stellten sich
F. Rosenblatt und seine Kollegen in den 50er Jahren [Ros62]. Mit ihrem
Perzeptron genannten Modell versuchten sie, Muster zu
erkennen. Allerdings wurde dem Perzeptron nicht gesagt, welche Muster es
erkennen soll. Vielmehr soll es diese Muster aus der Erfahrung heraus
erlernen. Abbildung 2.30 zeigt ein einfaches Perzeptron.
Lichtempfindliche Photorezeptoren propagieren Bits hin zu
![]() sogenannten Assoziationseinheiten. Letztere sind logische Schwellenwerteinheiten, wie sie auch schon von McCulloch und
Pitts verwendet wurden. Ein der Retina gezeigtes Muster erzeugt einen Vektor
sogenannten Assoziationseinheiten. Letztere sind logische Schwellenwerteinheiten, wie sie auch schon von McCulloch und
Pitts verwendet wurden. Ein der Retina gezeigtes Muster erzeugt einen Vektor
![]() von aktiven (
von aktiven ( ![]() ) und passiven
(
) und passiven
( ![]() ) Assoziationseinheiten. Die Verbindungsstruktur zwischen der
Retina und den Assoziationseinheiten ist als völlig beliebig angenommen.
Jede Assoziationseinheit propagiert nun über eine gerichtete und mit
) Assoziationseinheiten. Die Verbindungsstruktur zwischen der
Retina und den Assoziationseinheiten ist als völlig beliebig angenommen.
Jede Assoziationseinheit propagiert nun über eine gerichtete und mit
![]() gewichtete Verbindung ihre Ausgabe
gewichtete Verbindung ihre Ausgabe ![]() zu der Ausgabeeinheit. Die
Ausgabeeinheit ist wiederum eine logische Schwellenwerteinheit und ist somit
aktiv, sobald die Summe der gewichteten Eingaben den vorgegebenen Schwellenwert
übersteigt.
zu der Ausgabeeinheit. Die
Ausgabeeinheit ist wiederum eine logische Schwellenwerteinheit und ist somit
aktiv, sobald die Summe der gewichteten Eingaben den vorgegebenen Schwellenwert
übersteigt.
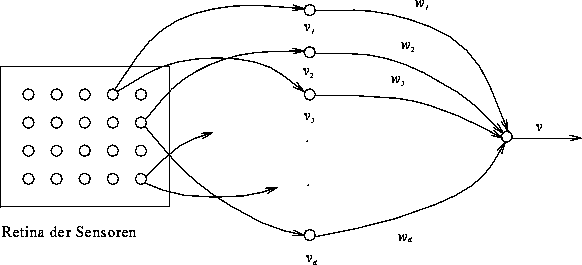
Abbildung 2.30: Ein einfaches Perzeptron mit d Assoziationseinheiten
und einer Ausgabeeinheit
Ein solches einfaches Perzeptron soll nun Klassifikationsprobleme
lösen, indem es der Retina vorgelegte Muster zwei verschiedenen
Klassen zuordnet. Als Beispiel sei ![]() . Somit haben wir als
mögliche von den Assoziationseinheiten erkannte Muster die
Vektoren
. Somit haben wir als
mögliche von den Assoziationseinheiten erkannte Muster die
Vektoren ![]() ,
, ![]() ,
, ![]() und
und ![]() . Sollen nun die
ersten drei Muster eine Klasse bilden, bei der die Ausgabeeinheit
passiv bleibt, und das letzte Muster eine Klasse bilden, bei der die
Ausgabeeinheit aktiv wird, dann realisiert das Perzeptron die
Konjunktion von
. Sollen nun die
ersten drei Muster eine Klasse bilden, bei der die Ausgabeeinheit
passiv bleibt, und das letzte Muster eine Klasse bilden, bei der die
Ausgabeeinheit aktiv wird, dann realisiert das Perzeptron die
Konjunktion von ![]() und
und ![]() . Abbildung 2.31 zeigt
ein solches Perzeptron. Die Zahlen an den Verbindungen von den Assoziationseinheiten zu der
Ausgabeeinheit dort sind die Gewichte dieser Konnektionen, und die Zahl in
der Ausgabeeinheit ist der Schwellenwert der Einheit.
. Abbildung 2.31 zeigt
ein solches Perzeptron. Die Zahlen an den Verbindungen von den Assoziationseinheiten zu der
Ausgabeeinheit dort sind die Gewichte dieser Konnektionen, und die Zahl in
der Ausgabeeinheit ist der Schwellenwert der Einheit.
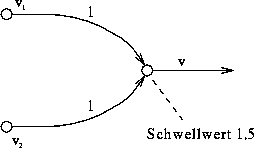
Abbildung 2.31: Das Perzeptron berechnet die Konjunktion
von ![]() und
und ![]() .
.
In Abbildung 2.31 sind die Gewichte noch vorgegeben. Das Perzeptron soll aber die Gewichte erlernen. Dazu legt man dem Perzeptron Muster vor und verändert die Gewichte nach einer bestimmten Regel, wenn das Muster falsch klassifiziert wurde. Rosenblatt konnte nun im sogenannten Konvergenztheorem für Perzeptronen zeigen, daß seine Modelle die korrekten Gewichte auf diese Weise erlernen konnten, wenn solche Gewichte überhaupt existierten. Minsky und Papert [MP72] fragten daraufhin, wann solche Gewichte existieren. In ihren Untersuchungen fanden sie dann viele einfache Beispiele, die ein Perzeptron prinzipiell nicht erlernen kann. Ein Perzeptron besteht ja nur aus einer Eingabe- und einer Ausgabeebene. Es kann also keine interne Repräsentation der vorgelegten Muster aufbauen. Vielmehr muß eine Klasse von Mustern eindeutig durch die Ähnlichkeit der Muster festgelegt sein. Das ist bei der Konjunktion gegeben, weil alle Elemente der einen Klasse mindestens eine Null enthalten. Beim ``ausschließlichen oder'' (XOR) aber bilden gerade die Muster (0,0) und (1,1) bzw. (1,0) und (0,1) je eine Klasse, und hier sind die Muster jeder Klasse gerade maximal verschieden.
Die Ergebnisse von Minsky und Papert führten zu einem schwindenden Interesse an künstlichen neuronalen Netzen. Erst gegen Ende der Siebziger Jahre hat das Gebiet eine Renaissance erlebt. Dies ist auf mehrere Gründe zurückzuführen.
Neuronen reagieren im Bereich weniger Millisekunden. Der Mensch reagiert im
Bereich einiger hundert Millisekunden mit durchaus komplexen Verhaltensweisen.
Das bedeutet, daß das komplexe Verhalten innerhalb von 100 Zeitschritten
generiert werden muß. Heute existierende KI-Programme benötigen
für vergleichbare Aktionen Millionen von Schritten. Nach Feldman und
Ballard [FB82] kann daraus nur folgen, daß das menschliche Gehirn
massiv parallel arbeiten muß. Ende der siebziger Jahre war es nun
gelungen, Rechner mit zigtausenden von Prozessoren zu bauen, so daß eine
massiv parallele Realisierung künstlicher neuronaler Netze in den Bereich
des Möglichen rückte.
Ende der siebziger Jahre war es nun
gelungen, Rechner mit zigtausenden von Prozessoren zu bauen, so daß eine
massiv parallele Realisierung künstlicher neuronaler Netze in den Bereich
des Möglichen rückte.
Zudem konnte J. J. Hopfield aus einfachen Schwellenwerteinheiten Netze
konstruieren, die sich als assoziative Speicher einsetzen ließen, die Fehler
bei der Eingabe korrigierten und die in VLSI-Technik realisiert werden
konnten [Hop82]. Hopfields Idee war der Physik entliehen. Er
betrachtete Systeme, deren Zustände durch Punkte eines
![]() -dimensionalen Raumes repräsentiert, also durch Vektoren
-dimensionalen Raumes repräsentiert, also durch Vektoren ![]() mit den Koordinaten
mit den Koordinaten ![]() gegeben sind. Bestimmte dieser
Zustände (zB. Minima) werden als stabile Zustände betrachtet.
gegeben sind. Bestimmte dieser
Zustände (zB. Minima) werden als stabile Zustände betrachtet.
Seien ![]() ,
, ![]() ,
, ![]() die stabilen Zustände
eines solchen Systems. Würde sich das System ausgehend von einem initialen
Zustand, der nahe zu einem dieser stabilen Zustände liegt (zB.
die stabilen Zustände
eines solchen Systems. Würde sich das System ausgehend von einem initialen
Zustand, der nahe zu einem dieser stabilen Zustände liegt (zB. ![]() ), in einem gewissen Zeitraum zu dem stabilen Zustand (hier
), in einem gewissen Zeitraum zu dem stabilen Zustand (hier ![]() ) ``hinbewegen'', dann könnte man davon sprechen, daß es die
Information
) ``hinbewegen'', dann könnte man davon sprechen, daß es die
Information ![]() speichert und in dieser Weise reproduzieren kann.
Insgesamt würde ein solches System zur Speicherung der Informationen
speichert und in dieser Weise reproduzieren kann.
Insgesamt würde ein solches System zur Speicherung der Informationen ![]() in der Lage sein. Jedes physikalische System,
dessen zeitliche Dynamik durch derartige stabile Zustände, die das System
anziehen, bestimmt wird, kann somit als inhaltsadressierbarer
Speicher aufgefaßt werden.
Hopfield konstruierte für eine Menge
in der Lage sein. Jedes physikalische System,
dessen zeitliche Dynamik durch derartige stabile Zustände, die das System
anziehen, bestimmt wird, kann somit als inhaltsadressierbarer
Speicher aufgefaßt werden.
Hopfield konstruierte für eine Menge ![]() von Vektoren ein neuronales
Netz und assoziierte mit dem Netz eine Energiefunktion
von Vektoren ein neuronales
Netz und assoziierte mit dem Netz eine Energiefunktion ![]() in der Weise,
daß jedem Vektor aus
in der Weise,
daß jedem Vektor aus ![]() ein lokales Minimum von
ein lokales Minimum von ![]() entspricht. Sodann definierte
er ein Verfahren (das Gradientenverfahren),
bei dem eine Einheit ihren Zustand dann ändert, wenn dadurch die Energie
des Gesamtnetzes verringert werden kann. Das Netz konnte somit, ausgehend von
einer partiellen und fehlerhaften Eingabe, die lokalen Minima der
Energiefunktion und damit die gespeicherten Vektoren finden.
entspricht. Sodann definierte
er ein Verfahren (das Gradientenverfahren),
bei dem eine Einheit ihren Zustand dann ändert, wenn dadurch die Energie
des Gesamtnetzes verringert werden kann. Das Netz konnte somit, ausgehend von
einer partiellen und fehlerhaften Eingabe, die lokalen Minima der
Energiefunktion und damit die gespeicherten Vektoren finden.
Als letzter Grund für die Renaissance künstlicher neuronaler Netze sei angefügt, daß es mehreren Gruppen gelungen war, eines der Hauptprobleme zu lösen, mit denen Perzeptronen nicht fertig werden konnten. Ein Perzeptron besteht ja nur aus zwei Ebenen von Einheiten, den Assoziations- oder Eingabeeinheiten und den Ausgabeeinheiten. Mit Hilfe der von Rosenblatt definierten Lernregel war es möglich, die Gewichte zwischen Ein- und Ausgabeeinheiten zu adaptieren. Um aber komplexere Funktionen wie etwa das XOR realisieren zu können, benötigt man weitere, sogenannte innere oder versteckte Ebenen zwischen der Ein- und Ausgabeebene. Dies ermöglicht eine Art Zwischenspeicherung, so daß keine direkte Ähnlichkeit mehr, wie oben erklärt, vorhanden sein muß. Ende der Sechziger Jahre kam niemand darauf, wie man die Gewichte zwischen den inneren Ebenen adaptieren sollte. Erst Hinton und Sejnowski lösten dieses Problem mit dem sogenannten Rückpropagierungs-Algorithmus [HS86]. Im Verlauf des Abschnitts wird darauf noch kurz eingegangen.
Zusammenfassend zeichnen sich künstliche neuronale Netze neben den oben genannten drei Prinzipien noch durch folgende Merkmale aus.

Jedes parallele, verteilte Prozessormodell (kurz
PVP-Modell, engl. PDP model) beruht auf einer
(großen) Menge von Einheiten. Die Bedeutung dieser Einheiten variiert
zwischen den einzelnen Modellen. In einigen können sie Zeichen, Worte und
Konzepte repräsentieren, in anderen handelt es sich um abstrakte Elemente,
aus denen sich solche Strukturen zusammensetzen. Sei ![]() die Anzahl der
Einheiten, die sich in beliebiger Weise als
die Anzahl der
Einheiten, die sich in beliebiger Weise als ![]() anordnen
lassen. In den folgenden Diagrammen werden dabei Einheiten als Kreise mit
mehreren Eingängen sowie einem Ausgang dargestellt. Jede Einheit
anordnen
lassen. In den folgenden Diagrammen werden dabei Einheiten als Kreise mit
mehreren Eingängen sowie einem Ausgang dargestellt. Jede Einheit
![]() besitzt ein Potential
besitzt ein Potential ![]() , dessen Werte unter den
verschiedenen Modellen variieren. Es kann sich dabei um
kontinuierliche
(zB. reelle Zahlen) oder diskrete (zB. binäre, natürliche Zahlen), um
beschränkte
oder unbeschränkte Werte eines eindimensionalen geordneten
Zustandsraumes handeln. Der Zustand des gesamten Systems wird durch einen
Vektor
, dessen Werte unter den
verschiedenen Modellen variieren. Es kann sich dabei um
kontinuierliche
(zB. reelle Zahlen) oder diskrete (zB. binäre, natürliche Zahlen), um
beschränkte
oder unbeschränkte Werte eines eindimensionalen geordneten
Zustandsraumes handeln. Der Zustand des gesamten Systems wird durch einen
Vektor ![]() dargestellt. Wie oben schon
ausgeführt, verfügt jede Einheit über eine endliche Anzahl von
gewichteten Eingängen und über einen Ausgang.
Abbildung 2.32 zeigt eine Einheit mit drei Eingängen, einem
Ausgang und ihrem Potential.
dargestellt. Wie oben schon
ausgeführt, verfügt jede Einheit über eine endliche Anzahl von
gewichteten Eingängen und über einen Ausgang.
Abbildung 2.32 zeigt eine Einheit mit drei Eingängen, einem
Ausgang und ihrem Potential.
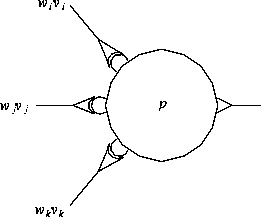
Abbildung 2.32: Eine Einheit u erzeugt in Abhängigkeit der
gewichteten Eingaben ![]() und Potentials
p eine Ausgabe v
und Potentials
p eine Ausgabe v
Die Einheiten sind über ein Geflecht von (gerichteten) Verbindungen
miteinander verkoppelt, was in Abbildung 2.33 illustriert ist. Ein
solches Geflecht entsteht, indem man den Ausgang einer Einheit mit den
Eingängen anderer Einheiten verknüpft, dh. der Ausgabewert ![]() einer Einheit wird zum Eingabewert anderer Einheiten. Je nachdem, ob die
Eingaben mit einem positiven oder negativen Gewicht versehen sind, erhält
man erregende oder hemmende Verbindungen. Der absolute Wert eines Gewichtes
gibt die Stärke an, mit der eine Einheit über die zugehörige
gerichtete Verbindung auf eine andere Einheit einwirkt. Empfängt eine
Einheit Eingaben, die nicht Ausgaben anderer Einheiten sind, dann spricht man
von einer
Eingabeeinheit. Erzeugt
eine Einheit Ausgaben, die nicht Eingaben für andere Einheiten sind, dann
spricht man von
Ausgabeeinheiten. Alle
anderen Einheiten heißen interne oder versteckte
Einheiten.
einer Einheit wird zum Eingabewert anderer Einheiten. Je nachdem, ob die
Eingaben mit einem positiven oder negativen Gewicht versehen sind, erhält
man erregende oder hemmende Verbindungen. Der absolute Wert eines Gewichtes
gibt die Stärke an, mit der eine Einheit über die zugehörige
gerichtete Verbindung auf eine andere Einheit einwirkt. Empfängt eine
Einheit Eingaben, die nicht Ausgaben anderer Einheiten sind, dann spricht man
von einer
Eingabeeinheit. Erzeugt
eine Einheit Ausgaben, die nicht Eingaben für andere Einheiten sind, dann
spricht man von
Ausgabeeinheiten. Alle
anderen Einheiten heißen interne oder versteckte
Einheiten.
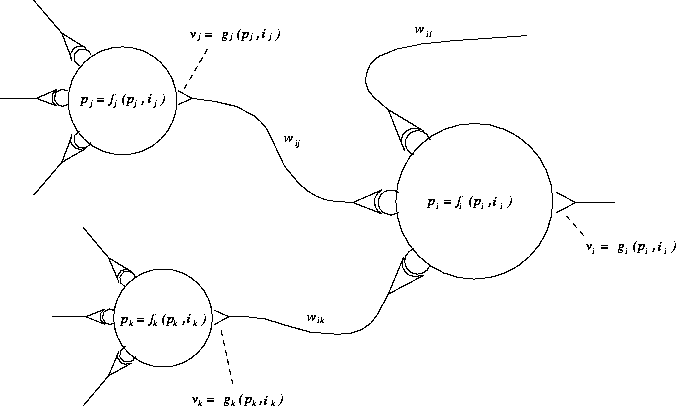
Abbildung 2.33: Ein Geflecht von drei Einheiten ( ![]() ))
))
Die Einheiten agieren nun (synchron oder asynchron), indem sie ihr
Potential gemäß ihrer Aktivierungsfunktion ![]() und ihre
Ausgabe gemäß ihrer Ausgabefunktion
und ihre
Ausgabe gemäß ihrer Ausgabefunktion
![]() berechnen. Dabei sind
berechnen. Dabei sind ![]() und
und ![]() , wie bereits gesagt,
einfache Funktionen. Als Beispiel haben wir schon die logischen
Schwellenwerteinheiten
kennengelernt, bei denen
, wie bereits gesagt,
einfache Funktionen. Als Beispiel haben wir schon die logischen
Schwellenwerteinheiten
kennengelernt, bei denen ![]() einfach die gewichtete Summe der Eingaben
berechnet und
einfach die gewichtete Summe der Eingaben
berechnet und ![]() eine Ausgabe erzeugt, wenn das Potential einen
vorgegebenen Schwellenwert übersteigt. Andere typische Funktionen sind zB.
die Identitätsfunktion, sigmoide Funktionen (dh.
differenzierbare und stufenartige
Funktionen)
oder stochastische Funktionen.
eine Ausgabe erzeugt, wenn das Potential einen
vorgegebenen Schwellenwert übersteigt. Andere typische Funktionen sind zB.
die Identitätsfunktion, sigmoide Funktionen (dh.
differenzierbare und stufenartige
Funktionen)
oder stochastische Funktionen.
Neuronale Netze sind wesentlich mit der Vorstellung verknüpft, Wissen in
einer Weise zu adaptieren, die uns beim Menschen wohlvertraut ist, nämlich
mittels Lernen und Erfahrung. Wie anders wäre es auch möglich,
zigtausende von Einheiten zu programmieren, dh. mit Initialwerten,
-funktionen und -verbindungen zu besetzen. Üblicherweise erfolgt das
Lernen über eine Veränderung der Verbindungsstruktur durch
Hinzufügen, Entfernen und Gewichtsveränderung von Verbindungen.
Insbesondere die letzte der drei Varianten, die ja die anderen beiden als
Spezialfälle umfaßt, findet viele Anwendungen. Die meisten davon folgen
in der einen oder anderen Weise der sogenannten Hebbschen Regel [Heb49]: Empfängt eine
Einheit ![]() Signale von
Signale von ![]() über eine mit
über eine mit ![]() gewichtete Verbindung und sind beide Einheit aktiviert, so wird das Gewicht
gewichtete Verbindung und sind beide Einheit aktiviert, so wird das Gewicht
![]() um
um ![]() verstärkt. Die
Konstante
verstärkt. Die
Konstante ![]() wird als Lernrate bezeichnet; je größer sie
ist, umso größer ist die Veränderung. Ebenso wie die gesamte
Modellfamilie mit den im vorangegangenen beschriebenen Merkmalen beruht auch
diese Regel auf neurophysiologischen Einsichten. So weiß man, daß
Synapsen in der Tat je nach Beanspruchung wachsen oder degenerieren
können, was als ``synaptische Plastizität'' bezeichnet wird.
wird als Lernrate bezeichnet; je größer sie
ist, umso größer ist die Veränderung. Ebenso wie die gesamte
Modellfamilie mit den im vorangegangenen beschriebenen Merkmalen beruht auch
diese Regel auf neurophysiologischen Einsichten. So weiß man, daß
Synapsen in der Tat je nach Beanspruchung wachsen oder degenerieren
können, was als ``synaptische Plastizität'' bezeichnet wird.
Von der Hebbschen Regel gibt es eine Reihe von Varianten
[RMt86]. Eine der bekanntesten ist die
Delta-Regel, die für den
folgenden Spezialfall eines zweistufigen Netzwerks, bestehend aus einer
Eingabe- und einer Ausgabeebene, definiert ist. Die Einheiten werden dabei als
linear angenommen, dh. ![]() . Ein solches Netz läßt sich nach dem
folgenden Algorithmus trainieren.
. Ein solches Netz läßt sich nach dem
folgenden Algorithmus trainieren.
![]()
und subtrahiere ![]() von
von ![]() , wobei
, wobei ![]() die von der
die von der ![]() -ten
Ausgabeeinheit produzierte Ausgabe,
-ten
Ausgabeeinheit produzierte Ausgabe, ![]() die von der
die von der ![]() -ten
Ausgabeeinheit gewünschte Ausgabe,
-ten
Ausgabeeinheit gewünschte Ausgabe, ![]() die Ausgabe der
die Ausgabe der ![]() -ten
Eingabeeinheit und
-ten
Eingabeeinheit und ![]() die Lernrate sind.
die Lernrate sind.
Das Verfahren bricht ab, wenn für alle Muster die gewünschte Ausgabe produziert wird. Es läßt sich zeigen, daß die in Schritt (e) angewendete Delta-Regel
![]()
den Fehler
![]()
für jedes vorgelegt Muster minimiert, wobei ![]() als Fehlerrate
bezeichnet wird. Für eine exakte Herleitung siehe [RHW86].
als Fehlerrate
bezeichnet wird. Für eine exakte Herleitung siehe [RHW86].
Diese Regel war schon in den Sechziger Jahren bekannt, und auch das schon
vorgestellte Perzeptron hat mit Hilfe einer vergleichbaren Regel gelernt. Das
Problem war nur, daß niemand wußte, wie die Delta-Regel erweitert
werden muß, damit die an der Ausgabeebene festgestellten Fehler in die
internen Ebenen eines mehrstufigen Netzes propagiert werden können. Dies
aber gelang zu Beginn der Achtziger Jahre mit Hilfe der verallgemeinerten
Delta- oder auch
Rückpropagierungsregel
(engl. backpropagation)
[RMt86]. Grundlage ist ein mehrstufiges
gerichtetes Netz ohne Rückkopplungen (engl. feedforward net) und eine
differenzierbare, monoton steigende Ausgabefunktion ![]() . Hier wollen wir
eine logistische Ausgabefunktion betrachten, dh.
. Hier wollen wir
eine logistische Ausgabefunktion betrachten, dh.
![]()
wobei ![]() eine einem
Schwellenwert vergleichbare Größe ist. Man beachte, daß
eine einem
Schwellenwert vergleichbare Größe ist. Man beachte, daß ![]() hier seine Extremwerte 1 und 0 nur annehmen kann, wenn die Gewichte unendlich
groß werden. Daher ist man bei dieser Ausgabefunktion zufrieden, wenn
hier seine Extremwerte 1 und 0 nur annehmen kann, wenn die Gewichte unendlich
groß werden. Daher ist man bei dieser Ausgabefunktion zufrieden, wenn
![]() die Werte 0.1 bzw. 0.9 annimmt. Wie bei den zweistufigen Netzen
wird ein Muster als Eingabe vorgelegt und gewartet, bis das Netz eine Ausgabe
produziert. Erneut vergleicht man die gewünschte mit der erzeugten Ausgabe
und berechnet
die Werte 0.1 bzw. 0.9 annimmt. Wie bei den zweistufigen Netzen
wird ein Muster als Eingabe vorgelegt und gewartet, bis das Netz eine Ausgabe
produziert. Erneut vergleicht man die gewünschte mit der erzeugten Ausgabe
und berechnet
![]()
Je nachdem wie die Fehlerrate
![]() aussieht, unterscheidet man zwei Fälle. Wenn die
aussieht, unterscheidet man zwei Fälle. Wenn die
![]() -te Einheit eine Ausgabeeinheit ist, dann erhält man
-te Einheit eine Ausgabeeinheit ist, dann erhält man
![]()
Für jede
interne Einheit ![]() berechnen wir das Fehlersignal rekursiv aus
den Fehlersignalen der Einheiten
berechnen wir das Fehlersignal rekursiv aus
den Fehlersignalen der Einheiten ![]() , zu denen
, zu denen ![]() propagiert,
dh.
propagiert,
dh.
![]()
Somit wird der Fehler, der an den Ausgabeeinheiten festgestellt wird, zu den Eingabeeinheiten zurückpropagiert. Für eine formale Herleitung sei erneut auf [RHW86] verwiesen. Obwohl ein Konvergenztheorem, wie für das Perzeptron und allgemeine zweistufige Netze, nicht bewiesen werden kann, zeigten Rumelhart, Hinton und Williams experimentell, daß viele der von Minsky und Papert in ihrer Kritik am Perzeptron vorgelegten Beispiele von einem mehrstufigen Netz durch Rückpropagierung gelernt werden können.
Die entscheidende Frage bei diesen Netzen, neben derjenigen der Lernmechanismen, ist die nach der Art der Repräsentation von Wissen. Die einfachste Form der Repräsentation ist die lokale, bei der jede Einheit grob gesprochen die Rolle eines Konzeptknotens eines assoziativen Netzes übernimmt. Offensichtlich läßt sich so jedes assoziative Netz durch Aktivierung einer entsprechenden Anzahl von Einheiten und durch Setzen der geeigneten Gewichte bei den vorhandenen Verbindungen repräsentieren.
Ein sehr stark vereinfachtes Beispiel entnehmen wir [Sha88]. In
Abbildung 2.34 sind hierarchisch angeordnete Konzepte und ihre
Eigenschaften als Rechtecke repräsentiert. Die dort dargestellten Dreiecke
sind zusätzliche Einheiten, die aktiv werden, sobald sie auf zwei ihrer drei
Eingabeverbindungen erregt werden. Das System soll aufgrund einer vorgegebenen
Menubestellung den passenden Wein dazu bestimmen. Dazu nehmen wir an, daß
Schinken bestellt wurde, dh. daß die mit SCHINKEN markierte rechteckige
Einheit (extern) aktiviert wurde. Wird nun die mit BESTELLE_WEIN markierte
ovale Einheit aktiviert und dessen Aktivierung entlang der eingezeichneten
Kanten durch das Netz propagiert, dann werden nacheinander die mit
BESTIMME_GESCHMACK und HAT_GESCHMACK bezeichneten Einheiten aktiv. Da nun
sowohl die mit SCHINKEN als auch die mit HAT_GESCHMACK bezeichnete Einheit
aktiv ist, wird die mit ![]() bezeichnete dreieckige Einheit aktiv werden.
Dies wiederum aktiviert die mit SALZIG und salzig bezeichneten Einheiten. Die
mit salzig, süß und weiß_nicht bezeichneten Einheiten sind in einem
sogenannten ``Alles-dem-Gewinner''- (engl. winner-take-all) oder kurz
WTA-Netz verknüpft. In einem solchen
Netz ``gewinnt'' die Einheit, die initial die größte Erregung erfährt,
dh. diese Einheit bleibt aktiv, während alle anderen Einheiten passiv
werden. In dem hier betrachteten Beispiel erfährt die mit salzig bezeichnete
Einheit die größte intiale Erregung. Als Folge davon schlägt das Netz
einen Rotwein vor.
bezeichnete dreieckige Einheit aktiv werden.
Dies wiederum aktiviert die mit SALZIG und salzig bezeichneten Einheiten. Die
mit salzig, süß und weiß_nicht bezeichneten Einheiten sind in einem
sogenannten ``Alles-dem-Gewinner''- (engl. winner-take-all) oder kurz
WTA-Netz verknüpft. In einem solchen
Netz ``gewinnt'' die Einheit, die initial die größte Erregung erfährt,
dh. diese Einheit bleibt aktiv, während alle anderen Einheiten passiv
werden. In dem hier betrachteten Beispiel erfährt die mit salzig bezeichnete
Einheit die größte intiale Erregung. Als Folge davon schlägt das Netz
einen Rotwein vor.
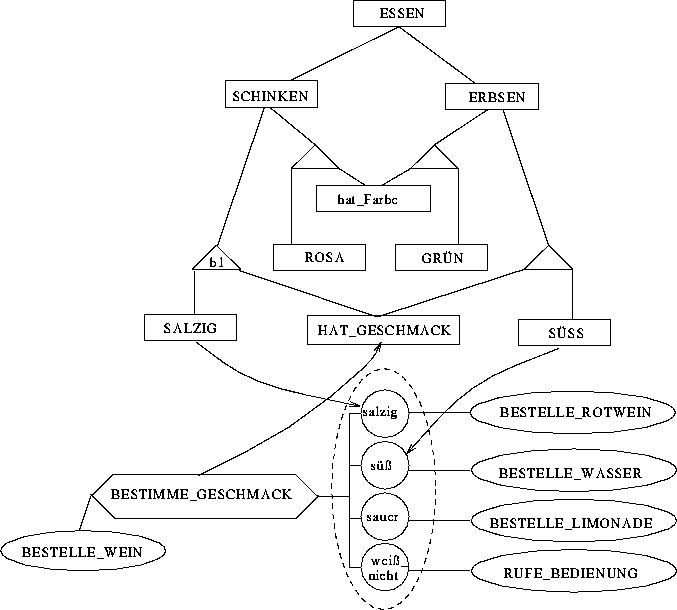
Abbildung 2.34: Ein einfaches semantisches Netzwerk
Es ist wenig wahrscheinlich, daß sich bei einer solchen Repräsentation ein signifikanter Unterschied zu konventionellen Modellen ergibt. Obwohl die Frage nach einem solchen Unterschied auch generell bis heute unbeantwortet ist, ließe sich doch denken, daß konnektionistische Maschinen in der folgenden Weise gegenüber konventionellen Maschinen in erster Näherung Vorteile aufweisen könnten, falls sich die vielen praktischen Schwierigkeiten überwinden ließen.
Logische Darstellungen werden oft als zu präzise kritisiert (und sind
wahrscheinlich bei dem menschlichen Hang zur Ungenauigkeit genau deswegen so
relativ unpopulär). Wenn wir ![]() als Faktum in der Wissensbasis
haben und
als Faktum in der Wissensbasis
haben und ![]() anfragen, so scheitert die Musterung, weil
anfragen, so scheitert die Musterung, weil ![]() und
und
![]() halt verschieden sind. Präzision kann dann preisgegeben werden,
wenn Raum für erhebliche Redundanz verfügbar ist. Betrachten wir das
Zeichen
halt verschieden sind. Präzision kann dann preisgegeben werden,
wenn Raum für erhebliche Redundanz verfügbar ist. Betrachten wir das
Zeichen ![]() als aus
als aus ![]() und einem Halbkreis bestehend und
und einem Halbkreis bestehend und ![]() noch
zusätzlich aus einem angehängten Strich, so sind bei Verwendung etwa
dreier Einheiten zur verteilten Darstellung von
noch
zusätzlich aus einem angehängten Strich, so sind bei Verwendung etwa
dreier Einheiten zur verteilten Darstellung von ![]() (hier aufgrund
eines simplen syntaktischen Kriteriums) zwei bereits durch das Zeichen
(hier aufgrund
eines simplen syntaktischen Kriteriums) zwei bereits durch das Zeichen ![]() aktiviert, was zu einem Musterungserfolg zwischen
aktiviert, was zu einem Musterungserfolg zwischen ![]() und
und ![]() führen kann. Entscheidend für den Erfolg ist bei dieser Sichtweise die
Überschreitung eines Schwellenwertes anstatt der Übereinstimmung in
ausnahmslos allen Merkmalen, was wiederum je nach Modell verschieden
realisiert wird.
führen kann. Entscheidend für den Erfolg ist bei dieser Sichtweise die
Überschreitung eines Schwellenwertes anstatt der Übereinstimmung in
ausnahmslos allen Merkmalen, was wiederum je nach Modell verschieden
realisiert wird.
Wäre es möglich, solche Schwellenwerte zudem empirisch durch geeignete Lernmechanismen festzulegen, so könnte sich eine konnektionistische Maschine möglicherweise eher zur Repräsentation und zur Verarbeitung von Wissen dieser Art eignen als eine konventionelle. Dies heißt aber immer noch nicht, daß man eine konnektionistische Maschine nicht durch eine konventionelle Maschine unter relativ wenig Effizienzverlust simulieren könnte. Schon das eben gegebene Beispiel läßt sich natürlich in gleicher Weise auch logisch formulieren, indem ein Axiom die Gleichheit von Prädikaten festlegt, die in mehr Merkmalen übereinstimmen, als ein vorgegebener Schwellenwert festlegt.
Ob in einem konnektionistischen Netz eine verteilte oder eine lokale Repräsentation von Wissen besser geeignet ist, muß derzeit als offenes Problem des Konnektionismus angesehen werden. Insbesondere hat man bislang keine überzeugende Lösung dafür angeben können, wie komplexe Wissensstrukturen repräsentiert und verarbeitet werden können [FP88]. Dies ist eine Frage, zu deren Lösung es auch von Seiten der Hirnforschung derzeit keinen hilfreichen Hinweis gibt. Deshalb werden eine Reihe von Ansätzen auf ihre Tauglichkeit hin untersucht [Hin90]. Solange es hier nicht zu einer Abklärung kommt, wird das Gebiet der Wissensrepräsentation nicht wirklich von diesen Ansätzen profitieren können.






Christoph Quix, Thomas List, René Soiron