Beispiel 11.3.1 (Kontextfreie Grammatik (CFG, context free grammar)).
- G1 = ⟨{S,NP,V P,EN,V,D,N},{Egon,Pudel,den,sah},R,S⟩
- Regelmenge
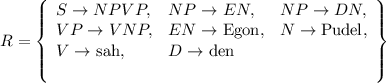
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Kontextfreie Phrasenstruktur-Grammatiken
Beispiel 11.3.1 (Kontextfreie Grammatik (CFG, context free grammar)).
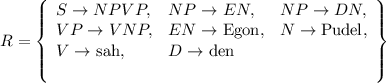
Definition 11.3.2 (Kontextfreie Grammatik). Eine Kontextfreie Grammatik G = ⟨Φ,Σ,R,S⟩ besteht aus:
Beispiel-Evaluation
Siehe Abb. 11.2 auf Seite 511.
Definition 11.3.3 (Direkte (oder unmittelbare) Ableitungsrelation).
Beispiel: Ableitung mit kontextfreier Grammatik
S1NP2VP2EN3Egon9V4 NP4 sah5 D6 N6 den7 Pudel8
| Ableitung | u | Regel | v |
| u1wu2 | w → z | u1zu2 | |
| S | 𝜖 S 𝜖 | S → NP VP | 𝜖 NP VP 𝜖 |
| ⇒ NP VP | 𝜖 NP VP | NP → EN | 𝜖 EN VP |
| ⇒ EN VP | EN VP 𝜖 | VP → V NP | EN V NP 𝜖 |
| ⇒ EN V NP | EN V NP | V → sah | EN sah NP |
| ⇒ EN sah NP | EN sah NP 𝜖 | NP → D N | EN sah D N 𝜖 |
| ⇒ EN sah D N | EN sah D N | D → den | EN sah den N |
| ⇒ EN sah den N | EN sah den N 𝜖 | N → Pudel | EN sah den Pudel 𝜖 |
| ⇒ EN sah den Pudel | 𝜖 EN sah den Pudel | EN → Egon | 𝜖 Egon sah den Pudel |
| ⇒ Egon sah den Pudel | |||
Definition 11.3.4 (Ableitung (derivation)). Eine Ableitung ist ein n-Tupel ⟨w1,…,wn⟩ von Zeichenketten wi ∈ Γ∗ mit (1 ≤ i ≤ n) , so dass gilt:
Normale Schreibweise für Ableitungen
w1 ⇒… ⇒ wn
Definition 11.3.5 (Ableitungsrelation (derivation relation)). Die Ableitungsrelation
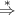 ist die reflexiv-transitive Hülle von ⇒. Sie verbindet alle Folgen von Symbolen, welche direkt oder
indirekt voneinander abgeleitet werden können.
ist die reflexiv-transitive Hülle von ⇒. Sie verbindet alle Folgen von Symbolen, welche direkt oder
indirekt voneinander abgeleitet werden können.
Definition 11.3.7 (Satz einer Grammatik). Eine Zeichenkette aus Terminalsymbolen w ∈ Σ∗ ist ein Satz einer Grammatik G = ⟨Φ,Σ,R,S⟩, gdw. er aus dem Startsymbol S abgeleitet werden kann:
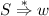
Definition 11.3.8 (Sprache einer Grammatik G). Die Sprache LG einer Grammatik G = ⟨Φ,Σ,R,S⟩ ist die Menge aller ihrer Sätze w ∈ Σ∗.
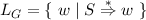
Äquivalente Grammatiken
Zwei Grammatiken heissen (schwach) äquivalent , wenn sie dieselbe Sprache erzeugen.
Grammatik-Regeln, Sprachklassen und Automaten
Die verschiedenen Grammatiktypen unterscheiden sich hinsichtlich der Bedingungen, die an die
Regelmenge R gestellt werden. Es seien A,B ∈ Φ,w ∈ Σ∗ und α,β,γ ∈ (Φ ∪ Σ)∗.
| Sprachklasse | Form der Grammatikregeln | Automatentyp | |
| Regulär | A → w | Endlicher Automat | |
| (Typ 3) | A → wB | oder A → Bw | |
| Kontextfrei | A → α | Kellerautomat | |
| (Typ 2) | |||
| Kontext- | αAγ → αβγ | mit β≠𝜖 oder | |
| sensitiv | S → 𝜖 | (dann darf S nicht | Linear |
| (Typ 1) | auf einer rechten Seite | beschränkter | |
| einer Regel vorkommen) | Automat (LBA) | ||
| (Typ 0) | α → β | (mit α≠𝜖 und α ⁄∈ Σ∗) | Turingmaschine |
Die Aufwand (Komplexität) der Berechnungen für das Parsen steigt von Typ 3 zu Typ 0 an.
Chomsky-Hierarchie [Hopcroft et al. 2002]
| Sprachklasse | Typ | Beispiel |
| regulär | 3 | {an} |
| kontextfrei | 2 | {anbn} |
| kontextsensitiv | 1 | {anbncn} |
| allgemein | 0 | |
Echte Teilmengen
Für alle Typ–i–Sprachen gilt: L3 ⊂ L2 ⊂ L1 ⊂ L0 .
Wo befinden sich natürliche Sprachen? [Hess 2005, 138ff.]
Mindestens Typ 2: NPnVPn (central embedding)
Mindestens Typ 1 nach [Shieber 1985, Kallmeyer 2005]: NPiNPjViVj (cross serial construction)
Komplexität, Grammatikalität, Akzeptanz von Sprache
Es darf daher getrost, was auch von allen, deren Sinne, weil sie unter Sternen, die, wie der Dichter
sagt, zu dörren, statt zu leuchten, geschaffen sind, geboren sind, vertrocknet sind, behauptet wird,
enthauptet werden, dass hier einem sozumaßen und im Sinne der Zeit, dieselbe im Negativen als
Hydra betrachtet, hydratherapeutischen Moment ersten Ranges, immer angesichts dessen, dass, wie
oben, keine mit Rosenfingern den springenden Punkt ihrer schlechthin unvoreingenommenen
Hoffnung auf eine, sagen wir, schwansinnige oder wesenzielle Erweiterung des natürlichen
Stoffeides zusamt mit der Freiheit des Individuums vor dem Gesetz ihrer Volksseele zu verraten
den Mut, was sage ich, die Verruchtheit haben wird, einem Moment, wie ihm in Handel,
Wandel, Kunst und Wissenschaft allüberall dieselbe Erscheinung, dieselbe Tendenz den
Arm bietet, und welches bei allem, ja vielleicht eben trotz allem, als ein mehr oder minder
undulationsfähiger Ausdruck einer ganz bestimmten und im weitesten Verfolge excösen
Weltauffasseraumwortkindundkunstanschauung kaum mehr zu unterschlagen versucht werden zu
wollen vermag - gegenübergestanden und beigewohnt werden zu dürfen gelten lassen zu müssen sein
möchte.
Christian Morgenstern, Vorrede zu Galgenliedern
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]