Definition 11.2.10. Eine formale Sprache L über Σ ist eine Teilmenge des Sterns von Sigma.
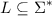
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Das Alphabet (Sigma), Zeichen und Zeichenketten
Definition 11.2.1. Ein Alphabet ist eine endliche Menge von Zeichen (atomare Symbole, Terminalsymbole). Es wird mit Σ (Sigma) notiert.
Beispiel 11.2.2 (Syntaktische Terminalsymbole des Englischen).
ΣEnglisch = {a,aardvark,…,cat,…,woman,…,zymurgy}
Definition 11.2.3. Eine Zeichenkette (formales Wort, string) von n Zeichen aus Σ ist eine endliche Folge der Länge n über Σ.
Definition 11.2.5. Die leere Zeichenkette (leeres Wort) ist die Folge von 0 Zeichen. Sie wird mit 𝜖 (Epsilon) notiert und hat die Länge 0.
Hinweis zur Notation
Eine Zeichenkette wird typischerweise durch Nebeneinanderschreiben (Juxtaposition) der Zeichen von links nach rechts notiert, wenn die Symbole nur aus einzelnen Buchstaben bestehen.
Sei Σ = {a,b}, dann sind etwa 𝜖, a, bb oder ababbba Wörter über Σ.
Wenn wir es in der Syntax mit Symbolen zu tun haben, welche aus mehreren Buchstaben bestehen, werden Leerzeichen zwischengeschaltet.
Definition 11.2.6. Der Stern von Sigma ist die Menge aller Zeichenketten über einem Alphabet Σ. Der Stern wird als Postfix-Operator Σ∗ (sprich «Sigma Stern») notiert.
Beispiel 11.2.8 (Sternbildung über Englisch).
| ΣEnglisch∗ = | |
| {𝜖, | Folge aus 0 Elementen |
| a,aardvark,cat,woman,… | Folgen aus 1 Element |
| a cat, cat a, peter sleeps,… | Folgen aus 2 Elementen |
| a a a, a cat sleeps, woman a cat,… | Folgen aus 3 Elementen |
| …} | Folgen aus n Elementen |
Grundfrage der Theorie der formalen Sprachen
Wie bestimmt man, ob eine Zeichenkette aus Σ∗ in einer Sprache ist oder nicht?
Beispiel 11.2.9. Sei Σ = {a}, dann ist Σ∗ = {𝜖,a,aa,aaa,…}. Die Mengen L1 = {𝜖,a} oder L2 = {aa,aaaa,aaaaaa} sind formale Sprachen, da sie (echte) Teilmengen von Σ∗ sind.
| ΣEnglisch∗ = | |
| {𝜖, | Folge aus 0 Elementen |
| a,aardvark,cat,woman,… | Folgen aus 1 Element |
| a cat, cat a, peter sleeps,… | Folgen aus 2 Elementen |
| a a a, a cat sleeps, woman a cat,… | Folgen aus 3 Elementen |
| …} | Folgen aus n Elementen |
Beispiel 11.2.11 (Abstrakt). Sei Σ = {a}. Die Mengen L1 = {𝜖,a} oder L2 = {aa,aaaa,aaaaaa} sind formale Sprachen, da sie (echte) Teilmengen von Σ∗ sind. Ist die leere Menge, notiert als {} oder ∅ eine Sprache? Ist sie dieselbe Sprache, wie die Sprache {𝜖}?
Beispiel 11.2.12 (Englisch). Wie können wir die gewünschte Teilmenge LEnglisch ⊆ ΣEnglisch∗ formal spezifizieren? Mit Regelgrammatiken.
Konkatenation von Zeichenketten
Definition 11.2.13. Die Konkatenation von Zeichenketten ist eine zweistellige Funktion, welche ihre Argumente in ihrer Reihenfolge zu einer Zeichenkette verkettet. Für alle u,v ∈ Σ∗:
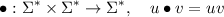
Beispiel 11.2.14 (Abstrakt: Zeichenketten verketten und aufteilen).
Was gibt: ab ∙ ba = abba oder abba ∙ 𝜖 = abba
Beispiel 11.2.15 (Englisch: Zeichenketten verketten und aufteilen).
Was gibt: a ∙ woman ∙ sees a ∙ cat = a woman sees a cat
Potenznotation der Konkatenation
Eigenschaften der Konkatenation
Die Konkatenation ist assoziativ und hat 𝜖 als neutrales Element . Für alle u,v,w ∈ Σ∗:
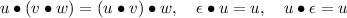
Definition 11.2.16. Die n-fache Konkatenation einer Zeichenkette w mit sich selbst in der Potenznotation sei rekursiv definiert. Für n ≥ 1,n ∈ ℕ:
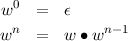
Beispiel 11.2.17 (Potenznotation der Verkettung).
Die Zeichenkette aaabbcccc kann als a3b2c4 notiert werden.
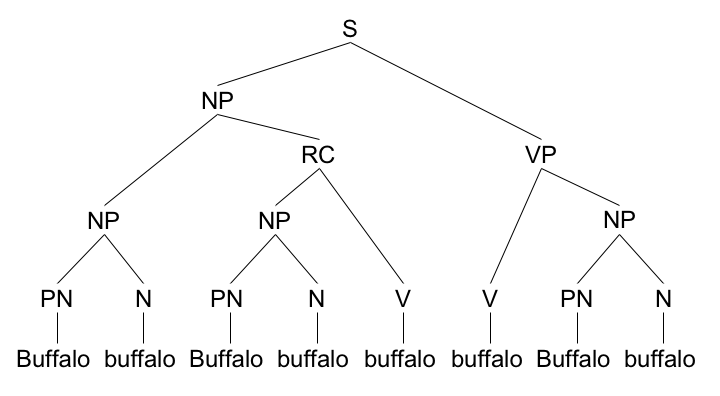
Beispiel 11.2.18 (Ein syntaktisch korrekter englischer Satz).
“Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo.”
Analyse
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]