Definition 5.3.1. Die Konkatenation von Relationen erweitert die Verkettung auf Mengen von Paaren von Zeichenketten. Für alle R,S ⊆ Σ∗× Σ∗:
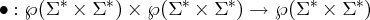
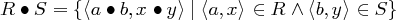
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Konkatenation von Sprach-Relationen
Definition 5.3.1. Die Konkatenation von Relationen erweitert die Verkettung auf Mengen von Paaren von Zeichenketten. Für alle R,S ⊆ Σ∗× Σ∗:
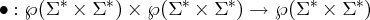
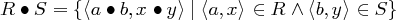
Beispiel 5.3.2. Sei R = {〈geb,gib〉,〈geb,gab〉} und S = {〈en,st〉}.
Dann ist
R ∙ S = {〈geben,gibst〉,〈geben,gabst〉}.
Stern einer Relation
Die Konkatenation von Relationen mit sich selbst erweitert sich wie bei den Sprachen zum Stern einer Relation.
Definition 5.3.3 (Binäre Relation). Eine Relation über Σ heisst regulär , wenn sie durch folgende reguläre Mengenausdrücke beschrieben werden kann:
Abschlusseigenschaften regulärer Relationen
Abschlusseigenschaften längengleicher regulärer Relationen
Reguläre Relationen, bei denen alle Paare von Zeichenketten gleich lang sind, sind abgeschlossen unter R1 ∩ R2 und R1 ∖ R2. Hinweis: Bei der Zwei-Ebenen-Morphologie mit Zwei-Ebenen-Regeln wird dies ausgenützt, indem das ε als ein Spezialsymbol verrechnet wird.
Reguläre Relationen und ET
Die Menge der regulären Relationen ist gleich der Menge der von ET akzeptierten Sprachen-Relationen.
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]