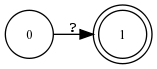
Beispiel 5.4.1 (ANY-Symbol in Sprache und Relation).
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Das kartesische Produkt in XFST
Wenn die RA A und B die Sprachen A und B über Σ bezeichnen, dann bezeichnet [ A .x. B ] die
Relation A × B.
Frage
Welche Relation beschreibt folgender Transduktor?
xfst[0]: read regex [{cat}|{dog}] .x. [{katze}|{hund}];
Universale Relation
Der RA [ ?* .x. ?* ] bezeichnet die universale Relation Σ∗× Σ∗, welche irgendeine Zeichenkette mit einer beliebigen andern paart.
Doppelpunkt-Operator
Anstelle von [ A .x. B ] kann auch [ A : B ] verwendet werden, der Doppelpunkt bindet einfach stärker. Er wird normalerweise für Symbolpaare verwendet a:b oder zusammen mit Klammernotation: {cat}:{chat}.
ANY-Symbol, Sprachen und Identitätsrelation
Jeder RA A für eine Sprache bezeichnet auch deren Identitätsrelation.
ANY-Symbol als Identitätsrelation
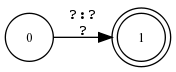
Der reguläre Ausdruck ? steht sowohl für die Sprache aller Zeichenketten der Länge 1 wie auch für die Identitätsrelation über dieser Sprache.
Wegen der Spezialbedeutung von ? steht ?:? nicht für die Identitätsrelation, sondern für Σ1 × Σ1.
Fallstrick: UNKNOWN-Kante vs. UNKNOWN-Paar-Kante
?:? als Kantenbeschriftung bedeutet zwingend unterschiedliche Symbole. Nur ? erlaubt identisches Symbolpaar.
Die unterschiedliche Verwendung des Fragezeichens in regulären Ausdrücken und endlichen Automaten ist bei ?:? besonders verwirrlich zugespitzt. Als regulärer Ausdruck (ANY) schliesst es die Identität ein, aber als Kante (UNKNOWN) schliesst es sie gerade aus. ?:? ist also eigentlich ein UNKNOWN:ANOTHERUNKNOWN.
Operator für Komposition von Relationen
Wenn die RA R und S die Relationen R und S über Σ bezeichnen, dann bezeichnet [ R .o. S ] eine
Relation. Sie beinhaltet ein Zeichenkettenpaar 〈u,w〉 genau dann, wenn R ein Paar 〈u,v〉 enthält und
S ein Paar 〈v,w〉.
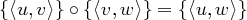
Beispiel 5.4.3 (Flexionsmorphologie mit Komposition und Ersetzung). Ein Beispiel für typisches Zusammenspiel von Komposition und Ersetzung bei der Behandlung eines Ausschnitts der regulären Verbflexion des Deutschen findet sich ▸▸▸hier.
Beispiele zur Komposition
Welche Sprach-Relationen bezeichnen die folgenden RA?
Hinweis
Die Komposition ist in XFST zusammen mit der Ersetzung ein fundamentaler Baustein und muss gründlich verstanden sein.
Hinweis
Auf EA angewendet verhält sich die Komposition identisch wie die Schnittmengenbildung:
A .o. B = A &
B.
Selbsttest Leichtes QUIZ zur Komposition:
http://www.cl.uzh.ch/ict-open/QUIZ/91
Operator für Ersetzung (replace)
Wenn die RA A und B die Sprachen A und B über Σ bezeichnen, dann bezeichnet [ A -> B ] eine
Relation. Sie besteht aus Paaren von beliebigen Zeichenketten, welche identisch sind, ausgenommen
aller Teilzeichenketten aus A in der oberen Sprache, die mit Teilzeichenketten aus B gepaart sein
müssen.
Hinweis zur Namensgebung des Operators
Falls B genau eine Zeichenkette enthält, werden alle Vorkommen von A durch B ersetzt.
Die Semantik des Ersetzungsoperators
Beispiel 5.4.5 (Ersetzung ▸▸▸). Gegeben sei die Relation [ [ a | b ] -> [ c | d ] ]. Welche Zeichenketten der unteren Sprache sind zur Zeichenkette eab aus der oberen Sprache gepaart?
Reduktion des replace-Operators
[ A -> B ] = [ NO_A [ A .x. B ] ]* NO_A ]
wobei
NO_A = ~ $ [ A - 0 ].
Eine beliebig wiederholte Konkatenation von Zeichenketten, welche nichts aus A enthalten, mit dem Kreuzprodukt von A und B. Gefolgt von beliebigen Zeichenketten, welche ebenfalls nichts aus A enthalten.
QUIZ Ersetzung und Komposition in Kombination
Optionale Ersetzung
Wenn die RA A und B die Sprachen A und B über Σ bezeichnen, dann bezeichnet [ A (->) B ] eine
Relation.
Sie besteht aus Paaren von beliebigen Zeichenketten, welche identisch sind. Zusätzlich können alle Teilzeichenketten aus A in der oberen Sprache mit Teilzeichenketten aus B gepaart sein.
Bedingte Ersetzung (conditional replacement)
Wenn die RA A, B, L und R Sprachen über Σ bezeichnen, dann bezeichnet
[ A -> B || L _ R ] eine
Relation.
Sie besteht aus Paaren von beliebigen Zeichenketten, welche identisch sind, ausgenommen aller Teilzeichenketten aus A in der oberen Sprache, die mit Teilzeichenketten aus B gepaart sein müssen, sofern sie nach L und vor R stehen.
Bedingte Ersetzung mit mehrfachen Kontexten
Anstelle nur eines einzigen möglichen Kontexts lassen sich beliebig viele durch Komma getrennt
angeben, in denen eine Ersetzung stattfinden muss:
[ A -> B || L1 _ R1 , L1 _ R1 , … , Ln _ Rn
]
Wortende verankern in Kontexten
Die Spezialmarkierung für Wortanfang/-ende
Die Kontexte in [ A -> B || L _ R , L1 _ R2 ] sind gegen Aussen implizit mit der universalen Sprache verkettet:
Im resultierenden ET ist .#. nicht vorhanden, es kann aber wie ein Symbol in die RA eingefügt werden.
Wegen der impliziten Erweiterung dürfen Kontexte auch fehlen.
ε in Kontexten: Zwecklos
Die leere Sprache in Kontexten
macht kaum Sinn:
[A -> B || 0 _ 0]
= [A -> B || ?* 0 _ 0 ?*]
= [A -> B || ?* _ ?*]
= [A -> B]
ε als Ersetzung: Wichtig und nützlich
Die leere Sprache als Ersetzung löscht die Zeichenketten der zu ersetzenden Sprache: [A -> 0]
ε als zu Ersetzendes: Überall und endlos
Die leere Sprache als zu Ersetzendes fügt an beliebiger Stelle beliebig oft das zu Ersetzende ein: [0 -> A]
Ein solcher ET besitzt ein ε-Loop auf der oberen Seite. Jeder Zeichenkette der oberen Sprache entsprechen unendlich viele Zeichenketten der unteren Sprache. (Automatisch prüfbar mit test upper-bounded in xfst.)
Einfügen als Einmal-Ersetzung (single insertion)
Das einmalige Einfügen von Zeichenketten ist wichtig und nützlich.
Gepunktete Klammern (dotted brackets)
In Ersetzungsausdrücken [ [. A .] -> B] beschränken gepunktete Klammern um das zu Ersetzende die Ersetzung von ε in A. An jeder Stelle darf es nur noch einmal ersetzt werden, d.h. B eingefügt werden.
Beispiel 5.4.10 (Einmal-Einfügen).
xfst[0]: regex [ [. 0 .] -> "+" ];
xfst[1]: apply down xyz +x+y+z+ xfst[1]: |
Beispiel 5.4.11 (Mehrfach-Einfügen).
xfst[0]: regex [ 0 -> "+" ];
xfst[1]: down xyz Network has an epsilon loop \ on the input side. ++x+y+z ++x+y+z+ ++x+yz ... |
Einfügen als Einmal-Ersetzung (single insertion)
Kurznotation
Der RA [..] wird gerne als Abkürzung für [. 0 .] verwendet.
ε-spezifische Wirkung
Die gepunkteten Klammern modifizieren die Ersetzung nur bezüglich ε. Die Ersetzung von nicht-leeren Teilzeichenketten besteht normal weiter.
Nicht-Determinismus in Ersetzung
Auch wenn in [ A -> B ] die Sprache B nur eine einzige Zeichenkette enthält, kann die Ersetzung
nicht-deterministisch sein.
Ursache 1: Unterschiedliche Länge der zu ersetzenden Sprache
Der ET aus [ [ a | a a ] -> b ] bildet etwa die obere Sprache {aa} auf {b,bb} ab.
Ursache 2: Überschneidende Ersetzungen
Der ET aus [ [ a b | b c ] -> z ] bildet etwa die obere Sprache {abc} auf {zc,az} ab.
Gerichtete Ersetzungsoperatoren mit Längenpräferenz
Ursache 1 des Nicht-Determinismus eliminieren
Ersetze nur die längste (->) oder kürzeste (>) Teilzeichenkette!
Ursache 2 des Nicht-Determinismus eliminieren
Ersetze nur von links nach rechts (@…) oder von rechts nach links (…@)!
Die 4 möglichen kombinierten Strategien
| von links | von rechts | |
| lang | A @-> B | A ->@ B |
| kurz | A @> B | A >@ B |
Siehe [KARTTUNEN 1996] zur Implementation dieser Operatoren.
Gerichtete Ersetzungsoperatoren
Fragen
Kopierendes Ersetzen (marking)
In Ersetzungsausdrücken kann ...
als Variable einmal dazu verwendet werden, die zu ersetzende Zeichenkette zu referenzieren.
Definition 5.4.13 (Marking). Wenn die RA A, B und C die Sprachen A, B und C über Σ bezeichnen, dann bezeichnet [ A -> B ... C ] eine Relation.
Sie besteht aus Paaren von beliebigen Zeichenketten, welche identisch sind, ausgenommen aller Teilzeichenketten aus A in der oberen Sprache, welche gepaart sind mit einer Kopie von sich selbst, die mit einem Präfix aus B und einem Suffix aus C verkettet ist.
Beispiel: Silbifizierung ▸▸▸
define C [b|c|d|f|g|j|h|k|l|m|n|p|q|r|s|t|v|w|x|z];
define V [a|e|i|o|u|y|ä|ö|ü]; define Silbifizierung [ C* V+ C* @-> ... "-" || _ C V ]; |
apply down silbe
apply down vorsilbe apply down leuchtplakat |
Ersetzungsoperatorvarianten
Neben den gezeigten Ersetzungsoperatoren gibt es noch weitere systematische Varianten
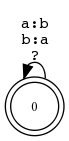
Parallele Ersetzung: Austauschen
Mehrere gleichzeitige Ersetzungen sind im Ersetzungsteil mit Komma getrennt möglich: [ A -> B , C
-> D , …, X -> Y ].
Beispiel 5.4.16 (xfst und Zustandsdiagramm).
read
regex
[
a
->
b,
b
->
a
]
;
apply
up
abba
baab
apply
down
abba
baab
read
regex
[a
->
b]
.o.
[
b
->
a]
;
apply
up
abba
apply
down
abba
aaaa
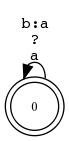
Zusammenspiel von Komposition und Ersetzung
Beispiel 5.4.17 (Der fiktionale Klassiker: kaNpat).
XFST-Skript ▸▸▸
define Rule1 [ N -> m || _ p ] ;
define Rule2 [ p -> m || m _ ] ; read regex Rule1 .o. Rule2 ; apply down kaNpat apply up kammat |
Definition 5.4.18 (Inversion von Relationen). Wenn R eine Relation darstellt, dann bezeichnet [ [ R ].i ] die Relation, bei der die obere und untere Sprache vertauscht sind.
Für alle Relationen R gilt: R = R.i.i.
Konstruktion eines inversen ET
Um aus einem ET einen neuen ET zu konstruieren, der die inverse Relation erkennt, müssen nur alle Symbole in den Symbolpaaren ausgetauscht werden.
Definition 5.4.19 (Projektion von Relationen auf Sprachen). Wenn R eine Relation darstellt, dann bezeichnet [ [ R ].u ] deren obere Sprache und [ [ R ].l ] deren untere Sprache.
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]