[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]

5.2.  Endliche Transduktoren

Endliche Transduktoren (ET)

Idee der endlichen Transduktoren

Endliche Transduktoren erweitern das Konzept des endlichen Automaten, indem auf zwei statt auf einem Band Zeichenketten verarbeitet werden.

Unterschiedliche Interpretationen der Bänder

Lexikalischer Transduktor bei Wortform-Generierung
Siehe Abb. 115 auf Seite 178.

pict

Abbildung 5.1: Lexikalischer Transduktor (von http://www.stanford.edu/~laurik/fsmbook/LSA-207/Slides/LSA2005-Lecture1.ppt)

Lexikalischer Transduktor bei Wortform-Analyse
Siehe Abb. 5.2 auf Seite 181.

pict

Abbildung 5.2: Lexikalischer Transduktor (von http://www.stanford.edu/~laurik/fsmbook/LSA-207/Slides/LSA2005-Lecture1.ppt)

5.2.1.  ε-NET

Nicht-deterministischer endlicher Transduktor (ε-NET)

Definition 5.2.1 (non-deterministic finite state transducer). Ein nicht-deterministischer endlicher Transduktor T = 〈Φ,Σ,δ,S,F〉 besteht aus

  1. einer endlichen Menge Zustände Φ
  2. einem endlichen Alphabet Σ
  3. einer Zustandsübergangsfunktion δ : Φ × Σε × Σε → ℘(Φ)
  4. einem Startzustand S ∈ Φ
  5. einer Menge von Endzuständen F ⊆ Φ

Hinweise

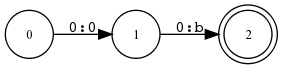
Die Notation Σε steht für Σ ∪{ε}, wobei ε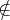∈∕Σ. Ein Transduktor unterscheidet sich nur in der Übergangsfunktion von einem EA.

ET im XFST-Prolog-Format

Beispiel 5.2.2 (Direktes Einlesen von ET im PROLOG-Format).

xfst[0]: read prolog  
        Type one or more networks in prolog format.  
        Use ^D to terminate input.  
arc(ex2,0,1,"0":"0").  
arc(ex2,1,2,"0":"b").  
final(ex2,2).

pict

Übergangsfunktion auf Paare von Zeichenketten
Die Bestimmung der Übergangsfunktion δ∗ auf Paare von Zeichenketten setzt auf der reflexiven und transitiven Hülle der ε:ε-Übergänge auf.

Definition 5.2.3. Die ε-Hülle δε∗ : Φ → ℘(Φ) eines ε-NET für einen Zustand T ∈ Φ ist rekursiv definiert durch:

pict pict

Abbildung 5.3: Rekursiver Erweiterungsschritt der ε-Hülle

Hinweis

Das Vorgehen ist analog zur Behandlung in ε-NEA.

Sprach-Relation von ε-NET

Definition 5.2.4 (Zustandsübergangsfunktion für Zeichenketten). Die auf Zeichenketten erweiterte Übergangsfunktion δ∗ : Φ × Σε∗× Σε∗→ ℘(Φ) bestimmt die Menge der erreichbaren Zustände nach dem vollständigen Lesen eines Paars von Zeichenketten.

Für alle T ∈ Φ,u,w ∈ Σ∗,x,y ∈ Σε (mit x,y ⁄= ε) eines ε-NET
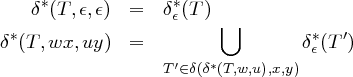
δ∗(T, ε,ε) = δ∗ε(T ) δ∗(T,wx, uy) = ⋃ δ∗(T′) ′ ∗ ε T ∈δ(δ(T,w,u),x,y)

Die Sprach-Relation eines ε-NET ist die Menge aller Paare von Zeichenketten, für die δ∗ ausgehend vom Startzustand mindestens einen Endzustand enthält.

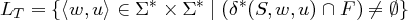
∗ ∗ ∗ LT = {〈w,u〉 ∈ Σ × Σ | (δ(S, w,u)∩ F ) ⁄= ∅}

5.2.2.  Zugrundeliegender EA eines ET

Zugrundeliegender EA
Jeder ET kann als EA aufgefasst werden, der die Symbole auf den beiden Bändern des ET als Symbolpaar auf einem Band verarbeitet.

Definition 5.2.5 (zugrundeliegender EA). Ein zugrundeliegender EA eines ET = (Φ,Σ,δ,S,F) ergibt sich als (Φ,Σ′,δ′,S,F): Für alle a,b ∈ Σ und T ∈ Φ

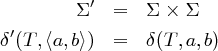
Σ ′ = Σ × Σ δ′(T,〈a,b〉) = δ(T,a,b)

5.2.3.  NET

Nicht-deterministischer endlicher Transduktor (NET)
Jeder ε-NET kann in einen äquivalenten NET umgewandelt werden, der keine ε:ε-Übergänge enthält, indem im zugrundeliegenden EA die entsprechende ε-Eliminierung gemacht wird.

Der NET kann jedoch weiterhin Übergänge vom Typ ε:a bzw. a:ε mit a ∈ Σ enthalten.

Beispiel 5.2.6 (Entfernen von ε:ε-Übergängen).

xfst[1]: epsilon-remove net  
xfst[1]: print net  
Sigma: b  
Flags: epsilon_free, loop_free  
Arity: 2  
s0 [non-det]: <0:b> -> fs1.  
fs1:  (no arcs)

pict

pict

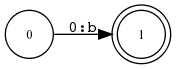
EA-Minimale Transduktoren in XFST
Das Minimieren von ET bezieht sich in XFST immer auf den zugrundeliegenden EA.

Beispiel 5.2.7 (xfst und Zustandsdiagramm).

xfst[0]: read regex [ a:0 0:b ] ;  
xfst[1]: minimize net  
xfst[1]: print flags  
deterministic, pruned, minimized, epsilon_free, loop_free,  

pict

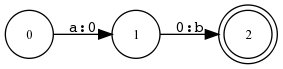
Hinweis

Die Relation kann leicht durch einen Automaten mit nur zwei Zuständen ausgedrückt werden. XFST führt eine solche Minimierung aber nicht automatisch durch. Für einfache Fälle der Form a:0 0:b führt der Stackbefehl cleanup allerdings doch noch zum erwünschten Ergebnis.

EA-Deterministische Transduktoren in XFST
Das Flag für Determiniertheit von ET bezieht sich in XFST immer auf den zugrundeliegenden EA.

Beispiel 5.2.8 (xfst und Zustandsdiagramm).

xfst[0]: set minimal OFF  
xfst[0]: read regex a:b c:a | a:b c:b;  
xfst[1]: print net  
...  
s0 [non-det]: <a:b> -> s1, <a:b> -> s2.  
...  
xfst[1]: determinize net  
xfst[1]: print net  
Flags: deterministic, pruned,  
       epsilon_free, loop_free

pict


pict

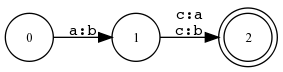
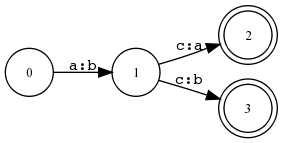
Hinweis

EA-Deterministische Transduktoren in XFST erlauben gleiche Symbole auf dem einen Band, welche zu unterschiedlichen Folgezuständen führen.

[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]