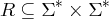
[ Weiter ] [ Seitenende ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]

5.1.  Formale Relationen

Formale Sprach-Relationen

Definition 5.1.1. Eine formale Sprach-Relation ist eine Teilmenge des kartesischen Produktes des Sterns von Sigma

R ⊆ Σ ∗ × Σ ∗
Eine Sprach-Relation ist also eine Menge von Paaren von Zeichenketten.

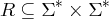
Beispiel 5.1.2. Sei Σ = {a,b,c,A,B,C}.
Dann ist beispielsweise R = {〈aa,AA〉,〈ab,AB〉,〈cc,CC〉} oder S = {〈Aaa,a〉,〈Aaa,aa〉,〈Aaa,c〉} eine formale Sprach-Relation über Σ.

5.1.1.  Sprach-Ebenen

Obere vs. untere Sprache

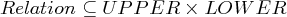
Relation ⊆ UP P ER × LOW ER

Definition 5.1.3 (Obere Sprache,upper language). Die obere Sprache umfasst alle Zeichenketten aus der 1. Komponente des kartesischen Produkts.

Sie enthält bei lexikalischen Transduktoren traditionell die abstrakte lexikalisch-morphologische Seite (lexical language).

Definition 5.1.4 (Untere Sprache, lower language)). Die untere Sprache umfasst alle Zeichenketten aus der 2. Komponente des kartesischen Produkts.

Sie enthält bei lexikalischen Transduktoren traditionell die Wortform .

Beispiel 5.1.5 (Obere und untere Sprache im Spanischen).
〈 cantar+Verb+PresInd+1P+Sg , canto〉∈ Rspanisch

Hinweis

Bei andern Ansätzen zur Morphologie mit endlichen Automaten wie [ANTWORTH 1990] bezeichnet man die Ebene der Wortformen mit surface form. Dies entspricht aber in XFST-Sprechweise der lower language!

5.1.2.  Identitätsrelation

Identitätsrelation einer Sprache
Sie ist eine technisch wichtige, inhaltlich aber uninteressante Relation und macht Sprachen zu Relationen, ohne an der Menge der erkannten Zeichenketten etwas zu ändern.
Obere und untere Sprache der Relation sind identisch mit der zugrundeliegenden Sprache.

Definition 5.1.6 (Identitätsrelation). Eine Identitätsrelation ID einer Sprache L über dem Alphabet Σ paart jede Zeichenkette der Sprache L nur mit sich selbst:
Für L ⊆ Σ∗:

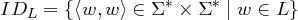
∗ ∗ IDL = {〈w,w 〉 ∈ Σ × Σ | w ∈ L }

Beispiel 5.1.7 (Identitätsrelation). Sei L = {canto,cantamos}.
Dann ist IDL = {〈canto,canto〉,〈cantamos,cantamos〉}.

[ Weiter ] [ Seitenbeginn ] [ Überkapitel ]              [ Bitte Skript-Fehler melden ]