
| Abbildung 4.2: | Deterministischer EA |
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ]
Deterministische Endliche Automaten (DEA)
Idee des akzeptierenden deterministischen endlichen Automaten
Ein endlicher Automat ist eine (abstrakte) Maschine zur zeichenweisen Erkennung von Wörtern einer regulären Sprache.
Beim Einlesen des ersten Zeichens einer Zeichenkette ist der Automat immer im sogenannten Startzustand.
Sie ist nach jedem Verarbeitungsschritt in genau einem Zustand.
Bei jedem Schritt wird ein Zeichen gelesen und aufgrund des aktuellen Zustands und dem Lesezeichen in einen Nachfolgezustand gewechselt. Wenn kein Zeichen mehr zu lesen ist und die Maschine in einem Endzustand ist, gilt die gelesene Zeichenkette als akzeptiert.
Wenn kein Übergang mit dem gelesenen Symbol möglich ist, gilt die zu verarbeitende Zeichenkette als nicht akzeptiert.
Deterministischer endlicher Automat (DEA)
Definition 4.2.1 (DEA, deterministic finite state automaton, DFA). Ein deterministischer endlicher Automat A = ⟨Φ,Σ,δ,S,F⟩ besteht aus
Hinweis
Die Übergangsfunktion δ bestimmt den Folgezustand, der ausgehend vom aktuellen Zustand beim Lesen eines einzelnen Zeichens erreicht wird.
Nicht-Deterministische Endliche Automaten (NEA)
Nicht-Determinismus I
Von einem Zustand geht mehr als eine Kante mit derselben Beschriftung weg.
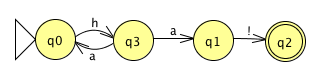
Nicht-Determinismus II
Es gibt mindestens eine ϵ-Kante.
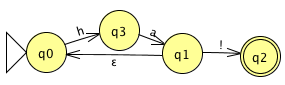
Wichtiges Resultat
Jeder Nicht-Deterministische Endliche Automat lässt sich in einen deterministischen verwandeln.

Konkatenation von Zeichenketten und Sprachen
Konkatenation von Zeichenketten
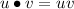
„work“ ∙ „ed“ = „worked“
Konkatenation von Sprachen
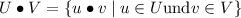
{ „work“} ∙ {„ed“, „s“} = {„work“∙„ed“, „work“∙„s“ }
= {„worked“, „works“ }

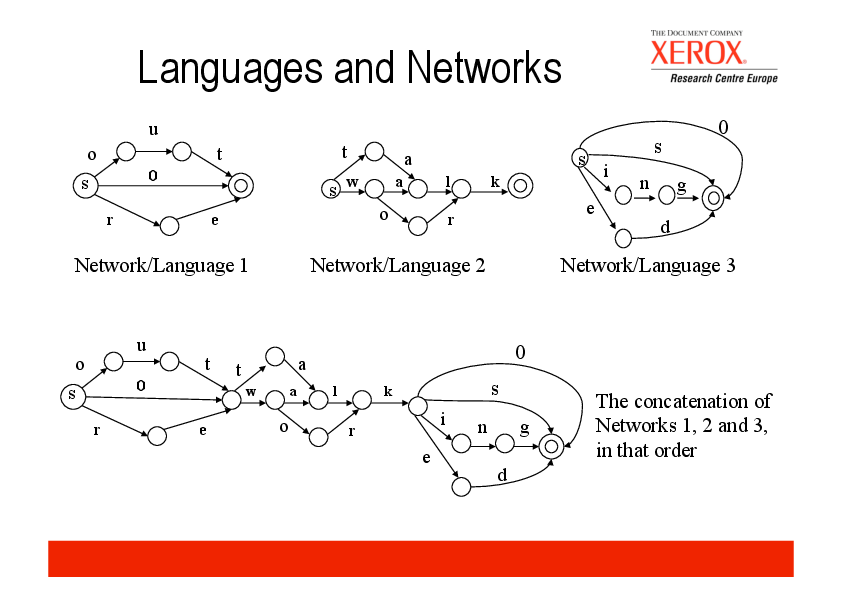
Quelle: B04
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ]