Formale Sprachen

Quelle: B04

Das Alphabet (Sigma): Menge von Zeichen

Definition 4.1.1. Ein Alphabet ist eine endliche Menge von Zeichen (atomare Symbole). Es wird mit Σ (Sigma) notiert.

Beispiel 4.1.2 (Zeichen des Englischen).
Σ_Englisch = {a,b,c,…,x,y,z}

Beispiel 4.1.3 (Zeichen der binären Zahlen).
Σ_bin = {0,1}

Zeichenketten (strings)

Definition 4.1.4. Eine Zeichenkette (formales Wort, string) der Länge n ist eine endliche Folge aus n Zeichen über Σ.

Beispiel 4.1.5 (Zeichenketten über englischen Symbolen Σ_Englisch).
a, we, work, and, talk, walk, krwrk,…

Leere Zeichenkette

Die leere Zeichenkette (leeres Wort) ist die Folge von 0 Zeichen. Sie wird mit ϵ (Epsilon) oder λ (Lambda) notiert und hat die Länge 0.

Sigma Stern

Σ^* ist die Menge aller Zeichenketten , welche aus dem Alphabet Σ gebildet werden können. Σ_bin^* = {ϵ,0,1,00,01,10,11,001,…}

Quelle: B04

Formale Sprachen als Teilmenge von Sigma Stern

* L ⊆ Σ

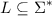
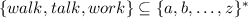
{walk, talk,work } ⊆ {a,b,...,z}*

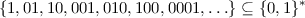
{1,01,10,001,010,100,0001,...} ⊆ {0,1}*

Wie lautet ein regulärer Ausdruck, der genau die Zeichenketten der obigen Sprache matchen kann?

Quelle: B04

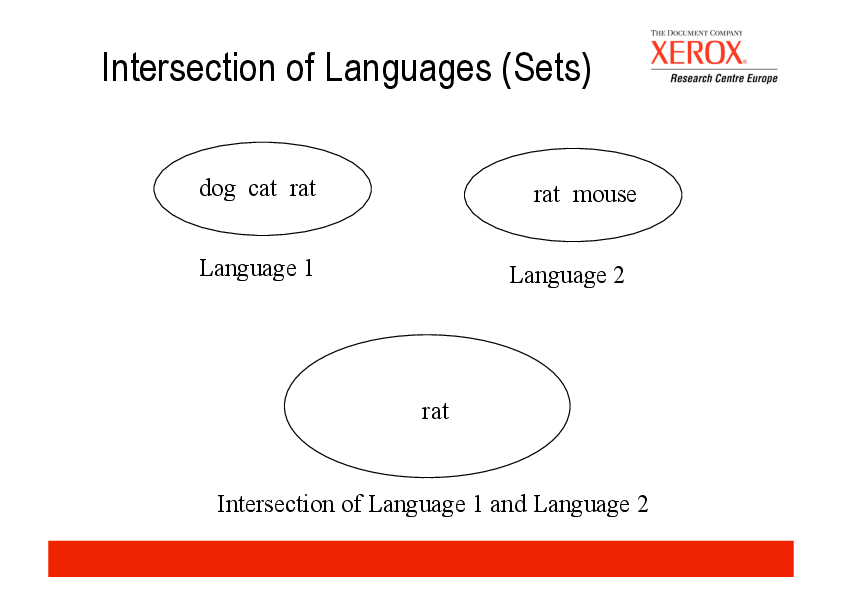
Ist eine Zeichenkette in einer Sprache drin oder nicht?

Abbildung 4.1:

Sprache aus 3 Verben

Beispiel 4.1.6.
Ist „talk“ ein Element der Sprache? Wahr oder falsch!

talk ∈ {work,talk,walk}

Endliche Automaten (EA) (engl. Finite-State Automatons (FA))

Endliche Automaten berechnen die Antwort auf diese Frage.