|
|
[ Weiter ] [ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Definition 12.1.1 (“Naive” Mengenlehre nach [CANTOR 1895]).
Kommentar zur Terminologie
Es gibt also Objekte , Mengen und Elemente .
Beispiel 12.1.2 (Mengen aus der Welt der Linguistik).
Menge der Sätze einer Zeitungausgabe, der Wortformen eines Satzes, der Lexeme eines Satzes, der
Buchstaben eines Wortes, der Bedeutungen eines Wortes, …
Definition 12.1.3 (Aufzählung einer Menge). Eine Mengenaufzählung besteht aus Zeichen(-ketten), welche die Objekte einer Menge bezeichnen und zwischen geschweiften Klammern stehen. Zwischen den Zeichen werden Kommata geschrieben. Die Reihenfolge der Zeichen ist irrelevant.
Beispiel 12.1.4 (Menge der Farben der französischen Flagge 
).
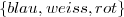oder {weiss,blau,rot} oder {bleu,blanc,rouge} oder {a,b,c}, falls z.B. festgelegt
ist, dass a für Rot, b für Blau und c für Weiss steht. Welche Konvention legt fest, dass bleu für die
Farbe Blau stehen soll?
Mehrfachschreibung von Zeichen
Die Notation {a,a,b,c,c,c} bezeichnet die gleiche Menge wie {a,b,c}.
Unterschiedliche Zeichen für dasselbe Objekt (Objektgleichheit)
Wenn gilt: a = b, dann bezeichnen {a,b} und {a} dieselbe Menge.
Beispiel 12.1.5 (Token).
Die Menge M der Token des Satzes “Wenn hinter Fliegen Fliegen fliegen, fliegt eine Fliege Fliegen
nach.”
M = {“Wenn”, “hinter”, “Fliegen”, “fliegen”, “,”, “fliegt”, “eine”, “Fliege”, “nach”, “.”}
Lexem als Menge von Token
LexemFliege = {“Fliege”, “Fliegen”}
Lexemverband als Menge von Lexemen
Lexemverbandflieg = {{“Fliege”,“Fliegen”}, {“fliegt”,“fliegen”,“fliegst”,…},…}
Definition 12.1.6 (Charakterisierung (Beschreibung) einer Menge). Eine Mengencharakterisierung besteht aus einer Variablen x (oder y,z), einem senkrechten Strich und einem Bedingungsteil, der angibt, unter welchen Bedingungen irgendein Objekt x Element der damit notierten Menge ist.
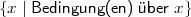
Gesprochen: Die Menge aller x, für die gilt: x … Die Variable x ist innerhalb der Klammern gebunden.
Beispiel 12.1.7 (Menge der Farben der französischen Flagge ).
{ x | x ist eine Farbe der französischen Flagge } { x | x ist die Farbe blau oder x ist die Farbe rot oder x ist die Farbe weiss }
Definition 12.1.8 (Notation der Elementbeziehung). Gehört ein Objekt x zur Menge A, so nennt man x ein Element der Menge A und schreibt x ∈ A.
Gehört y nicht
zur Menge A, schreibt man y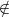
A.
Russelsche Paradoxie [IRVINE 2003]
Ob ein Objekt Element einer Menge ist oder nicht, lässt sich nicht in jedem Fall entscheiden. Sei M
die Menge, welche durch { x | x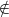
x } charakterisiert wird. Gilt M ∈ M?
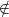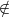M, so ist M ∈ M wegen der Mengencharakterisierung. Dies ergibt einen
Widerspruch.
M wegen der Mengencharakterisierung. Dies ergibt einen
Widerspruch.
Rekursiv charakterisierte Mengen
Mengen mit beliebig vielen Elementen
lassen sich rekursiv (induktiv) beschreiben.
Beispiel 12.1.9 (Natürliche Zahlen ℕ).
Verwendung von rekursiver Definitionen
Zeige, dass s(s(s(0))) Element der Menge der natürlichen Zahlen ist.
s(s(s(0))) ∈ ℕ, falls s(s(0)) ∈ ℕ (Rekursionschritt)
s(s(0)) ∈ ℕ , falls s(0) ∈ ℕ (Rekursionschritt)
s(0) ∈ ℕ, falls 0 ∈ ℕ (Rekursionschritt)
0 ∈ ℕ (Rekursionsbasis)
Logische Verknüpfungen und ihre Wahrheitswerte
|
|
Wahrheits- und Falschheitsbedingungen
|
|
Einige Wahrheits- und Falschheitsbedingungen
Sei m(x) das Prädikat “x ist menschlich” und s(x) das Prädikat “x ist sterblich”
Definition 12.1.10 (Extensionalitätsprinzip). Zwei Mengen M und N sind gleich , wenn sie die gleichen Elemente enthalten.
Formal: M = N = df.∀x(x ∈ M ↔ x ∈ N)
Beispiel 12.1.11 (Gleiche Mengen in beiden Notationsformen).
{a} = { x | x = a }
{a,b} = { x | x = a ∨ x = b }
Mengenungleichheit
Anstelle von ¬(M = N) schreibt man kurz: M ⁄= N.
Frage
In welchen Funktionen wird oben das Symbol “=” verwendet?
Definition 12.1.12 (Explizitdefinition nach [BUSSMANN 2002]). Bei Explizitdefinitionen enthält “das Definiendum neben dem zu definierenden Zeichen nur Variablen”. Sie “haben den Charakter von Abkürzungen”. Damit ist “die Forderung nach der Eliminierbarkeit der definierten Ausdrücke gewährleistet, d.h. die Reduzierbarkeit aller Aussagen auf die Grundbegriffe und die Axiome.”
Was für “Variablen”?
Die Definition der Mengengleichheit muss für beliebige Mengen gelten. Der Ausdruck
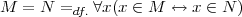
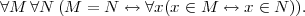
Definition 12.1.13 (Teilmenge, subset). Eine Menge M ist Teilmenge der Menge N, wenn jedes Element von M auch Element von N ist. Der Menge N sagt man Obermenge .
Formal: M ⊆ N = df.∀x(x ∈ M → x ∈ N)
Definition 12.1.14 (Echte Teilmenge, proper subset). Eine Menge M ist echte Teilmenge der Menge N, wenn M Teilmenge von N ist, aber nicht gleich N ist.
Formal: M ⊂ N = df.M ⊆ N ∧ M ⁄= N
Definition 12.1.16. Die leere Menge ist die Menge, welche keine Elemente enthält.
Formal: ∅ = df.{ x∣x≠x }
Alternativ-Notation: {}
Fragen
Ist die leere Menge Teilmenge jeder Menge?
Ist die leere Menge Element jeder Menge?
Definition 12.1.17 (power set). Die Potenzmenge einer Menge M ist die Menge aller Teilmengen von M.
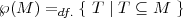
Alternativ-Notation: 2M
Beispiel 12.1.18.
Potenzmenge der Menge M = {1,2}
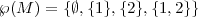
Hinweis: ∅ ist sowohl Element als auch Teilmenge von ℘(M).
Operationen über Mengen
Sei M = {a,b,c} und N = {c,d}:
Vereinigung
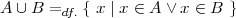
M ∪ N = {a,b,c,d}.
Schnittmenge
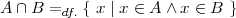
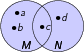
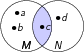M ∩ N = {c}
Disjunkte Mengen
Gilt A ∩ B = ∅, so haben A und B keine gemeinsamen Elemente und man nennt A und B disjunkt .
Sei M = {a,b,c} und N = {c,d} und G = {a,b,c,d,e}:
Differenz
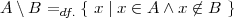
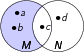M ∖ N = {a,b}.
Komplement
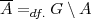
Kardinalität von endlichen Mengen
Definition 12.1.19. Die Kardinalität einer endlichen Menge A ist die Anzahl ihrer Elemente.
Formal: | A |
Beispiel 12.1.20.
Die Kardinalität der leeren Menge ist null: |∅| = 0.
Welche Kardinalität hat die Potenzmenge: | ℘(M) | =?
Unendliche Mengen
Mengen können auch unendlich viele Elemente enthalten. Z.B. die Menge der natürlichen Zahlen ℕ = {0,1,2,3,…}
[ Weiter ] [ Seitenbeginn ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
