Produktionsfunktion
Produktion ist der Prozess bei dem aus verschiedenen Inputs (zum Beispiel Rohstoffe) ein Output (das Produkt) generiert wird. Die Produktionsfunktion beschreibt dabei den Zusammenhang zwischen Input und Output und zeigt auf, wie viel mit einem gegebenen Input höchstens an Output produziert werden kann (Ewerhard Christian, 2007, Seite 202).
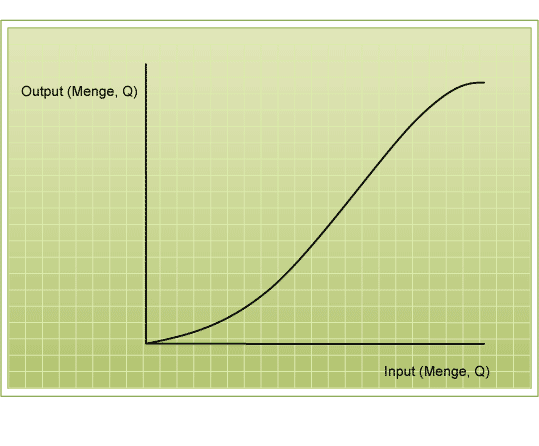Abbildung 8 - ProduktionsfunktionWir werden nun versuchen, die Produktionsfunktion in einem Diagramm einzuzeichnen. Zunächst gehen wir davon aus, dass die Produktionsfunktion einer steigenden Geraden entspricht.
Ist dies wirklich der Fall? Nehmen wir als Beispiel einen Konditor, welcher sich auf Schokoladenkuchen spezialisiert hat. Für einen Kuchen braucht er 500 Gramm an diversen Zutaten und eine Stunde (inkl. der Backzeit). Zutaten sowie Arbeitseinsatz (Arbeitszeit) sind der Input. Da gewisse Zutaten nur in grösseren Mengen erhältlich sind, wiegen diese insgesamt 800 Gramm (300 Gramm werden nicht gebraucht). Damit kann der Konditor nun einen Output (einen Kuchen) generieren. Was ist nun, wenn er sowohl die Zutaten als auch die Arbeitszeit verdoppelt - kann er dann doppelt so viele Kuchen herstellen? Mit 1600 Gramm an Zutaten und zwei Stunden Input wären drei Kuchen möglich (wenn der erste Kuchen im Backofen ist (Backzeit 30 Minuten) kann der Konditor bereits den nächsten Kuchen herstellen). Somit sind mit einer Verdoppelung des Inputs drei Kuchen möglich. Wir sehen, der Output ist überproportional grösser als der Input. Allerdings ist dies nur zu Beginn der Fall, wie wir der Kurve in Abbildung 9 entnehmen können. Grund dafür ist eine limitierende Ressource, in diesem Beispiel die Arbeitszeit des Konditors, denn diese können wir nicht unendlich vervielfachen.
Diesen Sachverhalt können wir auch mit Begriffen beschreiben. Die Durchschnittsproduktivität (AP, englisch für Average Productivity) beschreibt, wie viel Output (Kuchen) wir im Durchschnitt mit dem Input (Zutaten und Zeit) herstellen können. In der Abbildung 0 sehen wir, dass diese zunächst ansteigt (wir können mit mehr Input im Schnitt mehr herstellen) und ab einer gewissen Menge wieder sinkt.
Der zweite Begriff, den wir in diesem Zusammenhang gebrauchen können ist die Grenzproduktivität (MP, englisch für Marginal Productivity). Dieser Wert sagt, wie viel mehr Output wir mit einer Einheit Input mehr herstellen können. In anderen Worten, wie viele Kuchen können wir mehr produzieren, wenn wir die Zutaten und die Arbeitszeit verdoppeln? Die Grenzproduktivität entspricht mathematisch gesehen der Steigung der Produktionsfunktion. Der Abbildung 9 können wir entnehmen, dass die Grenzproduktivität zunächst ansteigt und dann wieder sinkt.
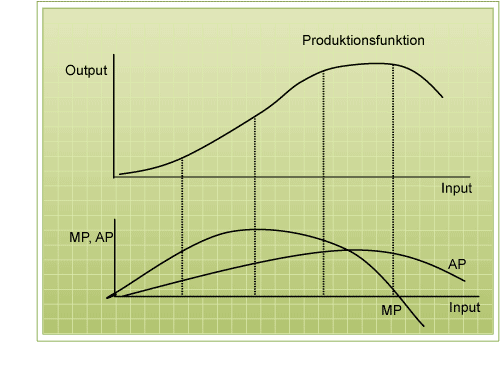Abbildung 9 - Produktionsfunktion, AP-Kurve, MP-Kurve
Ein weiteres Beispielfür die Produtktionsfunktion
Nehmen wir an, Sie betreiben ein kleines Unternehmen, welches T-Shirts mit einem vom Kunden gewünschten Logo bedruckt. Sie selbst können am Tag drei T-Shirts bedrucken (der gesamte Arbeitsvorgang beinhaltet das Waschen des T-Shirts, das Ausdrucken auf Spezialfolie des Logos, das Aufbügeln des Logos und das anschliessende Verpacken, inkl. Rechnungserstellung). Wenn Sie einen weiteren Mitarbeiter einstellen, können Sie 8 T-Shirts am Tag bedrucken. Sie sehen, eine Verdoppelung des Inputs (in diesem Falle die Anzahl der Mitarbeiter) erhöht die Anzahl des Outputs (die T-Shirts) um mehr als doppelt so viel. Die Grenzproduktivität ist somit grösser als 1 (doppelter Input generiert mehr als den doppelten Output). Ab einer gewissen Anzahl an Mitarbeiter sinkt die Grenzproduktivität jedoch wieder. Zum Beispiel, weil die Kapazität des Bügeleisens erreicht ist. Selbstverständlich wäre es auch möglich, sich ein weiteres Bügeleisen beschaffen und die Produktivität somit wieder steigern.
Die Grenzproduktivität (MP) gibt an, wie viel zusätzliche Einheiten an Output eine weitere Einheit Input generiert und entspricht somit der Steigung der Produktionsfunktion (erste Ableitung der Produktionsfunktion).
Die Durchschnittsproduktivität (AP) zeigt, wie viel Output mit einer Einheit Input im Durchschnitt erzeugt werden kann.