Optimierung
Optimierung bedeutet aus verschiedenen möglichen Lösungen die optimale (oder beste) Alternative finden. Während des Optimierungsprozesses wird eine Menge möglicher Lösungen auf eine Lösung oder wenige beste Lösungen reduziert.
Optimierung kommt in Situationen zur Anwendung, in denen Ressourcen wie Zeit oder Geld knapp sind. Ziel der Optimierung ist die maximale Ausnützung der verfügbaren Ressourcen.
Optimierung umfasst die folgenden drei Komponenten:
- eine Menge von Variablen,
- eine Menge von Beschränkungen und
- eine Menge von Objekten
Ein Beispiel für Optimierung wird später anhand der linearen Programmierung dargestellt.
Lineare Programmierung
Lineare Programmierung (LP) ist eine Optimierungstechnik, die häufig in EUS verwendet wird. Ziel der linearen Programmierung ist die optimale Zuteilung von Ressourcen auf konkurrierende Aktivitäten.
| Ein Problem im Sinne der linearen Programmierung besteht aus: | |
|---|---|
| Entscheidungsvariablen | Suche nach unbekannten Werten |
| Zielfunktion | Verknüpft die Entscheidungsvariablen mit dem Ziel, misst die Zielerreichung und muss optimiert werden |
| Zielfunktionskoeffizienten | Koeffizienten für Gewinn und Verlust pro Einheit, die angeben, wie stark eine bestimmte Entscheidungsvariable zum Ziel beiträgt |
| Beschränkungen | Dargestellt in Form von linearen Ungleichungen oder Gleichungen, die die Ressourcen und/oder Anforderungen beschränken |
| Kapazitäten | Beschreiben die Obergrenzen (manchmal auch die Untergrenzen) der Beschränkungen und Variablen |
| Koeffizienten | Zeigen die Ressourcennutzung für eine Entscheidungsvariable an |
Das Unternehmen "I4O" baut zwei verschiedene Computertypen. Derzeit steht die Entscheidung an, wie viele Computer vom Typ A und wie viele vom Typ B das Unternehmen im nächsten Monat herstellt.
Für die Herstellung von Typ A werden 300 Arbeitstage und $10.000 Materialkosten benötigt, während für Typ B 500 Arbeitstage und $15.000 Materialkosten anfallen.
Die Gewinnbeitrag jedes Computers vom Typ A liegt bei $8.000, vom Typ B bei $12.000. Pro Monat stehen 200.000 Arbeitstage und ein Materialbudget von $8.000.000 zur Verfügung.
Die Marketingabteilung hat festgestellt, dass pro Monat mindestens 100 Einheiten des Typs A und 200 Einheiten des Typs B produziert werden müssen.
Das Problem besteht nun darin, die Gewinne des Unternehmens zu maximieren, indem herausgefunden wird, wieviele Einheiten jedes Computertyps produziert werden sollen.
Das LP-Modell hat die folgenden drei Variablen:
1. Entscheidungsvariablen
X1 = zu produzierende Einheiten des Computertyps A
X2 = zu produzierende Einheiten des Computertyps B
2. Ergebnisvariablen
Totaler Gewinn = Z
Das Ziel ist, den Gewinn zu maximieren: Z = 8.000X1 + 12.000X2
3. Unkontrollierbare Variablen (Beschränkungen)
Arbeitsbeschränkung: 300X1 + 500X2 <= 200.000 (in Tagen)
Budgetbeschränkung: 10.000X1 + 15.000X2 <= 8.000.000 (in Dollar)
Marktbedarf für Typ A: X1 >= 100 (in Einheiten)
Marktbedarf für Typ B: X2 >= 200 (in Einheiten)
| Beschränkungen | A | B | Bez. | Grenze |
|---|---|---|---|---|
| Arbeit (Tage) | 300 | 500 | <= | 200.000/Monat |
| Material $ | 10.000 | 15.000 | <= | 8.000.000/Monat |
| Einheiten | 1 | >= | 100 | |
| Einheiten | 1 | >= | 200 | |
| Gewinn $ | 8.000 | 12.000 | Max |
Lösung
Zum Lösen dieses Problems soll das Programm MOPS (Mathematical Optimization System) dienen, welches an der Freien Universität Berlin entwickelt wurde. Es berechnet das optimale Ergebnis für unterschiedliche
Optimierungsaufgaben.
Eine in der Modellgrösse leicht eingeschränkte Version kann von der Homepage (http://www.mops.fu-berlin.de) kostenfrei unter "Demo Edition" heruntergeladen werden. MOPS wird als Excel-Add-In installiert und unter Excel als Makro
gestartet. Eine schrittweise Installationsanleitung ist in der beiliegenden Hilfe zu finden, die sich nach Ausführung der
Datei „clipmops.exe“ im MOPS-Ordner befindet.
Im Folgenden soll die Lösung der Computer-Aufgabe mit MOPS durchgeführt werden. Um das Beispiel besser nachvollziehen zu können, sollten Sie MOPS auf Ihrem PC installieren. Anschliessend starten Sie MOPS, indem Sie im Programmordner „clipMOPS“ wählen.
1. Schritt: Eingabe des Optimierungsmodells
Geben sie zunächst das Optimierungsmodell in Tabellenform in Excel ein, um es danach lösen zu können.
Damit MOPS die Daten auslesen und das Problem lösen kann, ist die Einhaltung einer festgelegten Form notwendig, welche in der folgenden Tabelle dargestellt ist.
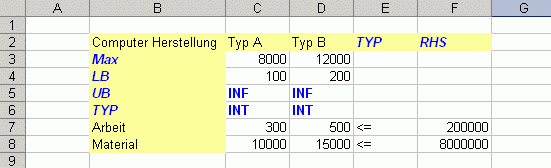 Fig. 8 - Das Optimierungsmodell als Tabelle
Fig. 8 - Das Optimierungsmodell als TabelleBezeichnungen im gelben Bereich beschriften die Tabelle. Blaue Bezeichnungen sind vorgegeben und werden durch MOPS interpretiert. Schwarze Bezeichnungen sind anwenderspezifisch. Die Formatierung der Schrift spielt für MOPS aber keine Rolle und dient hier nur der besseren Darstellung.
Zeile 7 entspricht z.B. der Gleichung der Arbeitsbeschränkung: 300X1(C7) + 500X2(D7) <=(E7) 200.000(F7). Der Wert in Zelle C7 sagt aus, dass für die Herstellung eines Computers von Typ A 300 Arbeitstage benötigt werden.
Folgende Bezeichnungen müssen in der Tabelle vorhanden sein:
In Zeile 2
| Bezeichnung | Interpretation |
|---|---|
| Computer Herstellung | Bezeichnung des Optimierungsmodells |
| Typ A und Typ B | Die unterschiedlichen Computertypen |
| TYP | Die Art der Beschränkung ( <=, >= , = ) |
| RHS (Right Hand Side) | Die Maximal- oder Minimalwerte der Beschränkungen (bezieht sich nur auf Arbeit und Material) |
In Spalte B
| Bezeichnung | Interpretation |
|---|---|
| Max | Zeile für die Zielfunktion/Gewinnfunktion (Max für Maximierung und Min für Minimierung) |
| LB (Lower Bound) | Die untere Grenze für die Anzahl der Computer |
| UB (Upper Bound) | Die obere Grenze für die Anzahl der Computer (INF steht für unendlich, d.h. es können theoretisch unendlich viele Computer produziert werden) |
| TYP | Der Typ der Entscheidungsvariablen (hier INT für ganzzahlige Werte, da es keine halben Computer geben kann) |
| Arbeit | legt fest, wieviel Arbeitszeit ein Computer für die Herstellung benötigt |
| Material | legt fest, wieviel die Materialkosten für einen Computer betragen |
Geben Sie die Tabelle, wie in Abbildung 8 dargestellt, ein.
Schritt 2: Lösung des Optimierungmodells
Nach Eingabe der Tabelle, kann die Optimierung durchgeführt werden. Dazu gehen Sie im Menü unter MOPS auf „Optimieren...“.
Wenn man mit der Tabelle in Zelle B2 begonnen hat, sollte MOPS den Bereich automatisch richtig auswählen, ansonsten makiert
man ihn manuell. Um die Berechnung zu starten, bestätigt man den Dialog mit „OK“.
Die folgende Abbildung zeigt den Dialog „Optimieren“ sowie unter der Tabelle das berechnete Ergebnis.
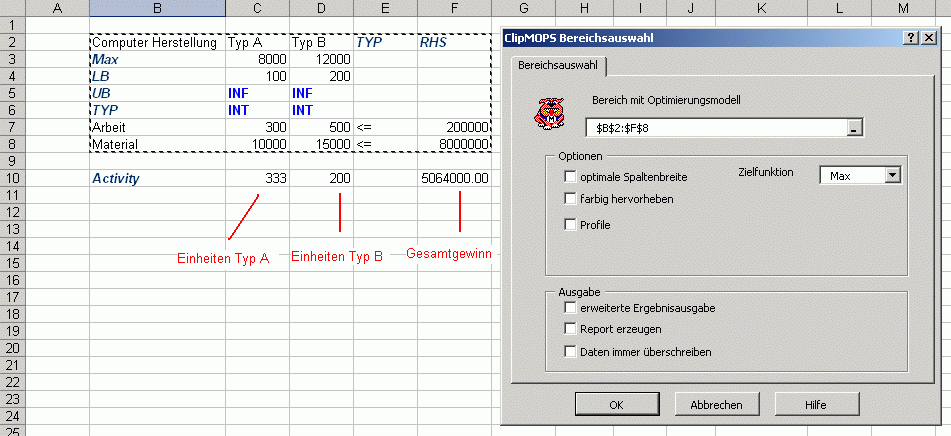 Fig. 9 - Der Optimierungsdialog und das Ergebnis
Fig. 9 - Der Optimierungsdialog und das ErgebnisErgebnis
Das Ergebnis unter der Tabelle sagt aus, dass man 333 Einheiten von Computer A (Typ A) und 200 Einheiten von Computer B (Typ
B) produzieren sollte, um den Gesamtgewinn zu maximieren, welcher im Optimum 5.064.000 Dollar beträgt.
X1 = 333
X2 = 200
Z = 5.064.000
Aufgabe: Letzigrund
Sie können nun die folgende Aufgabe mit Hilfe von MOPS lösen. Die Lösung finden Sie am Ende der Lerneinheit.
Im Stadion Letzigrund soll ein Fussballspiel stattfinden. Maximal stehen für die Zuschauer 10.000 qm an Platz zur Verfügung. Es können entweder Stehplätze zu 15 Franken, oder Sitzplätze zu 35 Franken angeboten werden. Die maximale Anzahl der Sitzplätze beträgt 1.500, da nicht mehr Stühle vorhanden sind. Stühle lassen sich hinzufügen und entfernen. Ein stehender Fussballfan benötigt 1 qm Platz und ein sitzender Fussballfan 2 qm.
Wieviele Steh- und Sitzplätze sollten verkauft werden und wie hoch ist dabei der maximale Gewinn?