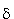 ) ist gegeben durch:
) ist gegeben durch:
Morphologieanalyse und Lexikonaufbau (5. Vorlesung)
Dozent: Martin VolkZwei-Ebenen-Morphologie ist eine Theorie zur Beschreibung morphologischer Phänomene von K. Koskenniemi, insbesondere zur Beschreibung der Gesetzmässigkeiten an Morphemgrenzen. Seine Grundannahmen:
Lit.: [Covington 94] Kap. 9, [Sproat 92], [Koskenniemi 84], [Trost 91]
Beispiel: Bildung der Form 2. Sg Präsens vom Verb rasen
Ausgangsform: r a s + s t
| | | | | |
Oberflächenform: r a s 0 0 t
Benötigt wird also ein Formalismus, der eine Ausgangsform in eine Oberflächenform (und umgekehrt) übersetzen kann. Dazu benutzt man einen sog. Transducer. Dies ist eine Sonderform eines endlichen Automaten, der gleichzeitig durch zwei Zeichenketten läuft.
[Dieser Abschnitt ist entnommen aus: Informatik-eine grundlegende Einführung in vier Teilen (Teil IV), Manfred Broy: 1.3.2 Endliche Automaten]
**************** Beginn des übernommenen Abschnitts ******************
Endliche Automaten sind ein sehr
einfaches Modell für informationsverarbeitende Maschinen.
Ein endlicher Automat A
= (S, T, s0, Sz, 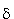 ) ist gegeben durch:
) ist gegeben durch:
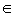 S,
S,
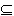 S von Endzuständen,
S von Endzuständen,
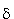 : S
: S 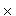 (T
(T 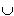 {
{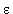 })
}) 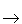
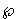 (S).
(S).Sind die Werte der Übergangsfunktion höchstens einelementig und gilt
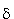 (s,
(s, 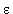 )
) 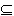 {s}
{s}
für alle s 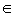 S, so heißt
der Automat deterministisch,
sonst nichtdeterministisch.
Ist
S, so heißt
der Automat deterministisch,
sonst nichtdeterministisch.
Ist 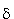 (s, a) (für a
(s, a) (für a 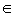 T) stets verschieden von der leeren
Menge, so heißt der Automat total,
sonst partiell.
T) stets verschieden von der leeren
Menge, so heißt der Automat total,
sonst partiell.
Ein endlicher Automat läßt sich einfach durch einen durch Teilmengen aus T kantenmarkierten Graphen über der Menge der Zustände darstellen. Es existiert eine Kante vom Zustand s1 zum Zustand s2, falls gilt
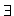 a
a 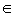 T
T 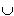 {
{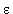 }: s2
}: s2
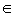
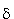 (s1, a) .
(s1, a) .
Dann wird die Kante mit der Menge
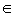 T
T 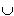 {
{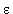 }: s2
}: s2
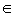
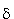 (s1, a)}
(s1, a)}
markiert. Diese Graphen nennen wir Transitionsgraphen oder auch Zustandsübergangsgraphen.
Beispiel(Endlicher Automat). Wir führen einen endlichen deterministischen Automaten durch Angabe seiner Bestandteile ein:
| Zustandsmenge | S = {s0, s1, sf}, | |
| Eingangszeichen | T = {a, b}, | |
| Anfangszustand | s0, | |
| Endzustände | Sz = {s1}. |
Die Übergangsfunktion wird durch
die Tabelle 1.2 beschrieben.
Diese Information können wir
auch durch die graphische Darstellung des Automaten in Abb. 1.18
wiedergeben.
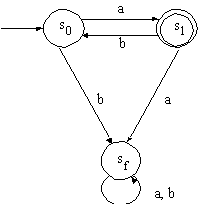
Aus diesem Transitionsgraph können wir die Bestandteile des Automaten ablesen. Wir kennzeichnen den Anfangszustand mit einem unmarkierten Pfeil ohne Quelle und Endzustände durch doppelte Kreise.
Gilt für einen Zustand sf
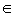 S:
S:
 t
t 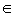 T
T 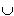 {
{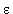 }:
}: 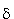 (sf,
t)
(sf,
t) 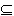 {sf},
{sf},
**************** Ende des übernommenen Abschnitts ******************
Ein endlicher Automat ist ein Formalismus, der beschreibt, wie durch die Abarbeitung von Symbolen von einem Zustand in einen anderen Zustand gewechselt wird. Man kann einen endlichen Automaten nutzen, um einfache Morphemfolgen zu beschreiben. Also z.B. die Abfolge von Verbstamm plus Endung.
{schwimm,zeig}+{e,st,t,en}
Zur Beschreibung der Besonderheiten bestimmter Stämme (z.B. Stamm endet auf -s wie bei rasen), benötigt man entweder eine Klasseneinteilung (mit entsprechenden Endungslisten) oder die Zwei-Ebenen-Morphologie.
Der Nutzen eines endlichen Automaten wird noch deutlicher bei der Beschreibung der Abfolge mehrerer Suffixe. Z.B. bei Adjektiven die Abfolge von Komparations- und Flexionssuffix (Beispiel: schön+er+em) oder, wie im folgenden Automaten, bei mehreren Derviationssuffixen. Dabei steht N_i für eine Unterklasse aller Substantive, die das Derivationssuffix -los nehmen (z.B. Kopf, Hilf) und V_i für eine Unterklasse aller Verben (genauer: Verbstämme), die eine Substantivierung mit dem Suffix -ung bilden können (z.B. bedeuten, wirken).
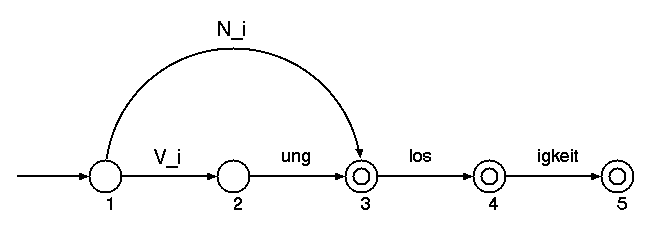
Gute Hintergrundinformationen zu endlichen Automaten, Beispiele und bewegte Abläufe bietet die Projektseite Visualisierung endlicher Automaten.
Die von endlichen Automaten akzeptierten Sprachen lassen sich durch einfache Ausdrücke beschreiben, die als reguläre Ausdrücke bezeichnet werden. Sei T eine endliche Menge von Eingangszeichen (auch Alphabet genannt). Dann werden die regulären Ausdrücke über T wie folgt definiert:
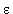 ist ein regulärer Ausdruck.
ist ein regulärer Ausdruck.
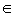 T ist für sich ein regulärer Ausdruck.
T ist für sich ein regulärer Ausdruck.
Merke:
(r+) = (r(r*))
(r?) = (r | 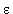 )
)
[Der folgende Abschnitt ist entnommen aus: Informatik - eine grundlegende Einführung in vier Teilen (Teil IV), Manfred Broy: 1.3.4 Reguläre Ausdrücke, endliche Automaten und Chomsky-3-Sprachen]
**************** Beginn des übernommenen Abschnitts ******************
Satz: Zu jedem regulärem Ausdruck können wir einen nichtdeterministischen endlichen Automaten angeben, der die durch den regulären Ausdruck angegebene Sprache akzeptiert.
Beweis: Wir realisieren den regulären Ausdruck durch endliche Automaten mit genau einem Anfangszustand, einem Endzustand und ohne Kanten, die in den Anfangszustand oder aus dem Endzustand führen. Wir geben für jede Form, die ein regulärer Ausdruck haben kann, induktiv einen endlichen Automaten an. Wir benennen zur Vereinfachung der Darstellung die Zustände nicht.
(1) Für den regulären Ausdruck
x mit x 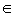 T verwenden wir den Automaten aus Abb. 1.24.
T verwenden wir den Automaten aus Abb. 1.24.
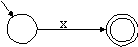
Für den regulären
Ausdruck 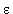 verwenden wir den Automaten aus Abb. 1.25.
verwenden wir den Automaten aus Abb. 1.25.
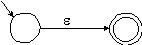
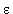 } akzeptiert
} akzeptiert
Für den regulären
Ausdruck {} verwenden wir den Automaten aus Abb. 1.26.

(2) Seien X und Y reguläre
Ausdrücke mit den Automaten in Abb. 1.27.
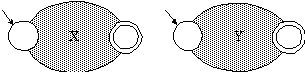
Für den regulären
Ausdruck [X|Y] verwenden wir den Automaten in Abb. 1.28.

Für den regulären Ausdruck [XY] verwenden wir den Automaten in Abb. 1.29.
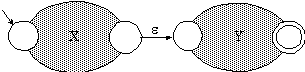
Für den regulären Ausdruck X* verwenden wir den in Abb. 1.30 angegebenen Automaten.
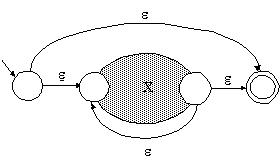
Die angegebenen Automaten beschreiben offensichtlich jeweils die gleiche formale Sprache wie die zugehörigen regulären Ausdrücke. Ein exakter mathematischer Beweis läßt sich durch Induktion über die Struktur des regulären Ausdrucks führen.
**************** Ende des übernommenen Abschnitts ******************
Wichtig: Es gelten folgende Äquivalenzen:
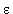 -Transitionen (N
-Transitionen (N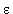 -FSA) überführt werden (wie oben gesehen).
-FSA) überführt werden (wie oben gesehen).
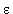 -Transitionen (N
-Transitionen (N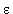 -FSA) kann in einen äquivalenten nichtdeterministischen endlichen Automaten (N-FSA) überführt werden.
-FSA) kann in einen äquivalenten nichtdeterministischen endlichen Automaten (N-FSA) überführt werden.
Während ein endlicher Automat eine Sprache über einem Alphabet mit einfachen Symbolen (z.B. T = {a,b,c}) akzeptiert, akzeptiert ein Transducer eine Sprache über Paaren von Symbolen (z.B. T = {a:a, b:b, c:c, a:b, a:0, 0:c}). Diese Eigenschaft macht man sich zu Nutze, um in der Morphologie den Zusammenhang zwischen Ausgangsstruktur und Oberflächenstruktur zu beschreiben.
Bsp.:
T = {a:0, a:a, b:b}
RegExpr = "a:a* a:0 b:b*"
Akzeptiert z.B. : <aaabbb, aabbb>, <a, 0>, <abb, bb>
Akzeptiert nicht: <aaabbb, aaabbb>, <bb, bb>
* steht für null oder mehr + steht für 1 oder mehr 0 steht für ein leeres Symbol
Ein Transducer (wie auch ein FSM) kann durch eine Übergangstabelle repräsentiert werden.
Tabelle: (in der linken Spalte stehen durchnumeriert die Zustände; ein Doppelpunkt deutet an, dass es sich um einen Endzustand handelt; der Zustand '1' ist der Anfangszustand; Ø steht für einen Fehlerzustand)
a a b a 0 b --------------------------- 1. 1 2 Ø 2: Ø Ø 2
Die Paare in einer Transducer-Tabelle können so interpretiert werden, dass jeweils der erste Buchstabe zu einer (hypothetischen) Ausgangsform (engl. lexical form oder underlying form) gehört und der zweite Buchstabe jeweils ein Bestandteil der Oberflächenform (engl. surface form) ist. Man spricht auch von einem Eingabe- und einem Ausgabeband. Da jedoch die Richtung unbestimmt ist, kann die Interpretation wechseln.
Problem: Wie geht man vor, wenn die Anwendung eines FST die Anwendung eines anderen FST auslöst?
Die Regel: Ein Anfangs-s einer Flexionsendung wird eliminiert, wenn der Verbstamm auf s, x oder z endet. (Bsp.: ras+st -> rast, mix+st -> mixt). pi steht für beliebige Paare.
T = {s:s, s:0, x:x, z:z, +:0}
RegExpr = "pi+ (s:s | x:x | z:z) +:0 s:0 pi+"
Ein Beispielprogramm in Prolog.
T = {t:t, t:0, +:0}
RegExpr = "pi+ t:t +:0 t:0 pi*"
Merke: Transducer sind in ihrer Funktion als Analysator (oder Generator) nicht immer deterministisch (d.h. ihre Implementation erfordert Backtracking)
Bsp.:
T = {x:a, x:b, a:a, b:b}
RegExpr = "(x:a* a:a) | (x:b* b:b)"
Akzeptiert: <xxxa, aaaa>, <xxxxb, bbbb>
x x a b
a b a b
------------------------------------
1. 2 3 Ø Ø
2. 2 Ø 4 Ø
3. Ø 3 Ø 4
4: Ø Ø Ø Ø
Bei Eingabe von xxxxa kann der Transducer erst bei a entscheiden, ob er den richtigen Pfad gewählt hat.
(nach [Sproat 92] S. 145): Um morphologische Phänomene eleganter beschreiben zu können, als das mit regulären Ausdrücken möglich ist, führt Koskenniemi einen Regelformalismus auf einer höheren Abstraktionsebene ein. Diese Regeln nennt er Two-Level-Regeln, kurz TWOL-Regeln. Solche Regeln können automatisch in Transducer übersetzt werden.
TWOL-Regeln haben die Syntax:
CP op LC _ RC
mit
a:b /<= LC _ RC
a:b => LC _ RC
a:b <= LC _ RC
a:b <=> LC _ RC
Hier beispielhaft gezeigt für eine Surface Coercion Regel (nach [Sproat 92] S.154-156). Seien b und v Buchstaben und V die Menge aller Vokale. Dann heisst:
b:v <= V:V _ V:V
b muss durch v ersetzt werden, wenn davor und dahinter ein Vokal auftritt. Die Vokale werden durch die Regelanwendung nicht geändert.
pi* V:V (b:b|b:p) V:V pi*wobei pi* die Menge der möglichen Paare symbolisiert.
pi* V:V (b:b|b:p)und
Bsp. (aus [Trost 91] S.428) ein Anfangs-s in einer Flexionsendung wird eliminiert, wenn der Stamm auf s, x oder z endet. (ras+st -> rast, mix+st -> mixt)
s:0 <=> {s:s x:x z:z} +:0 _
Bsp. (aus [Trost 91] S.439) ein Schwa-e muss eingefügt werden zwischen Stamm, der auf d oder t endet und Flektionsendung, die mit s oder t beginnt. (rast+st -> rastest, red+st -> redest)
+:e <=> {d:d t:t} _ {s:s t:t}
"Uml a~ä" a:ä <=> _\[%#: | a: | o: | u:]* @U:; _u: \[%#: | a: | o: | u:]* @U:;
"Uml u~ü" u:ü <=> \a: _\[%#: | a: | o: | u:]* @U:;
Hintergrund-Informationen zu PC-Kimmo
PC-KIMMO>rec hospitalization
`hospital+ize+ation `hospital+VR6+NR23
1:
Word
|
Stem
_____|______
Stem SUFFIX
____|____ +ation
Stem SUFFIX +NR23
| +ize
ROOT +VR6
`hospital
`hospital
Word:
[ cat: Word
clitic:-
head: [ number:SG
pos: N ]
lemma: `hospital
lemma_pos:N
nonreg:- ]
1 parse found
PC-KIMMO>
Beispieldatei (in Auszügen) mit Zwei-Ebenen-Regeln für das Englische.
;english.rul
;Rules file for Englex
;last modified 2-Mar-95
;Copyright (C) 1991-1995, Summer Institute of Linguistics, Inc.
;CONTENTS
;Defaults
;Epenthesis
;y:i-spelling
;Elision
;Gemination
;END
;s-deletion
;i:y-spelling
;' = apostrophe
;- = hyphen
;` = stress
;+ = morpheme break
ALPHABET
b c d f g h j k l m n p q r s t v w x y z a e i o u ' - ` +
NULL 0
ANY @
BOUNDARY #
SUBSET C b c d f g h j k l m n p q r s t v w x y z
SUBSET Csib s x z
SUBSET Cpal c g
SUBSET V a e i o u
SUBSET Vbk a o u
RULE "Defaults" 1 31
b c d f g h j k l m n p q r s t v w x y z a e i o u ' - + ` @
b c d f g h j k l m n p q r s t v w x y z a e i o u ' - - 0 @
1: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
RULE "Defaults" 1 16
+ y 0 e 0 0 0 0 0 0 0 0 0 0 0 @
0 i e 0 b d f g l m n p r s t @
1: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
;y:i-spelling
RULE " y:i => @:C (+:0)_+:0" 4 5
y @ e + @
i C 0 0 @
1: 0 2 1 1 1
2: 3 2 4 4 1
3. 0 0 0 1 0
4: 3 2 1 4 1
RULE " y:i /<=
@:C (+:0)_+:0 [i|']" 5 7
@ y e + ' i @
C i 0 0 ' i @
1: 2 1 1 1 1 1 1
2: 2 3 5 5 1 1 1
3: 2 1 1 4 1 1 1
4: 2 1 1 1 0 0 1
5: 2 3 1 1 1 1 1