[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenende ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]
Definition 13.2.1 (Unifikationsgrammatik nach [Bussmann 2002]). Unifikationsgrammatik (unification grammar) ist ein „Grammatikmodell, das auf einer Weiterentwicklung des linguistischen Merkmals basiert. Jede linguistische Einheit (Wort oder Phrase) ist durch eine Merkmalstruktur gekennzeichnet.“
Verhältnis Phrasenstruktur vs. Merkmalstruktur
PATR-II [Shieber 1992]
Definition 13.2.2 (PArsing and TRanslation). Der PATR-II-Formalismus ist ein Grammatik-Formalismus mit hoher Theorieneutralität (Werkzeugformalismus).
Komponenten von PATR-II
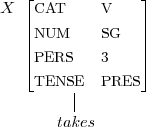
Lexikonregel (partiell)
X → takes
⟨X CAT⟩ = V
⟨X NUM⟩ = SG
⟨X PERS⟩ = 3
⟨X TENSE⟩ = PRES

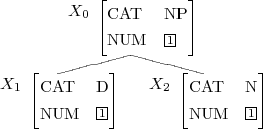
Syntaxregel mit Numerus
X0 → X1 X2
⟨X0 CAT⟩ = NP
⟨X1 CAT⟩ = D
⟨X2 CAT⟩ = N
⟨X0 NUM⟩ = ⟨X1 NUM⟩
⟨X0 NUM⟩ = ⟨X2 NUM⟩
XLE-Formalismus
Der XLE-Formalismus unterstützt die Grammatikmodellierung in der Tradition der LFG
(Theorieformalismus). LFG enthält 2 verschiedene Repräsentationsebenen:
Relativ theorieunabhängige Komponenten von XLE
Etwas gewöhnungbedürftige Notation für Referenz auf Merkmalstrukturen von Mutterknoten (LFG:↑; XLE:^) und Tochterknoten (LFG:↓; XLE:!).
Lexikonregel (partiell)

Syntaxregel mit Numerus
![[ ]
N P NUM 1-
[ |] [ |-]
D NUM 1- N NUM -1](script124x.png)
Definition 13.2.3 (Kongruenz, engl. Agreement). Kongruenz : Übereinstimmung zwischen zwei oder mehreren Satzelementen hinsichtlich ihrer morpho-syntaktischen Kategorien (Kasus, Person, Numerus, Genus). [Bussmann 2002]
Kongruenz in Grammatikformalismen
Kongruenz lässt sich in Unifikationsgrammatiken durch Pfadgleichungen ausdrücken.
Phänomene der Numerus-Kongruenz im Englischen
Kongruenzen in Numerus
Frage
Wie lauten die Merkmalsgleichungen in den Grammatikregeln?
Kongruenz II
Kongruenzphänomene mit weiteren Kategorien
Definition 13.2.4 (Rektion, government). Rektion : Lexemspezifische Eigenschaft von Verben, Adjektiven, Präpositionen oder Substantiven, die die morphologische Kategorie (insbesondere den Kasus) abhängiger Elemente bestimmt. Rektion kann unter Valenz subsumiert werden, insofern Valenzträger die morphologische Form der von ihnen ’regierten’ (abhängigen) Elemente bestimmen (’regieren’). [Bussmann 2002]
Definition 13.2.5 (Valenz, Subkategorisierung). Valenz
ist die Fähigkeit eines Lexems, seine syntaktische Umgebung vorzustrukturieren, in dem es
anderen Konstituenten im Satz Bedingungen bezüglich ihrer grammatischen Eigenschaften
auferlegt. [Bussmann 2002]
Verben gleicher Valenz werden oft in Subkategorien
aufgeteilt.
Frage
Wie lässt sich Rektion in Unifikationsgrammatiken ausdrücken? Rektion/Valenz wird durch Merkmalspezifikation ausgedrückt.
Lexikalisierung
Viel Rektions-Information stammt aus den Lexikoneinträgen.
Aus Gründen der Übersichtlichkeit sind nicht alle morphosyntaktischen Merkmale aufgeführt.
Minigrammatik in XLE mit minimalen Merkmalen
Diskussion der Umsetzung in XLE
Aufgrund der Phrasenstruktur zulässige, aber inkorrekte Sätze werden ausgefiltert.
Probleme
Ziel einer vollständigen F-Struktur-Repräsentation
Kopfprinzip
Funktionalisierung von Nicht-Köpfen
Tochterkonstituenten, welche nicht Köpfe ihrer Mutter sind, werden in ihrer Funktion bezüglich dem Kopf bestimmt und als Unterstruktur integriert.
Typische Funktionen
Demo von syntaktischen Funktionen in LFG: http://decentius.aksis.uib.no/logon/xle.xml Die Frage, was ist der Kopf, ist nicht immer einfach zu beantworten. Beispiele?
Minigrammatik in XLE mit minimalen Merkmalen
Die Köpfe sind erkennbar an ^=!. Die Nicht-Köpfe an (^FUN)=!.
Mengenwertige Merkmale
XLE (und andere Unifikationsgrammatiken) erlauben oft zusätzliche Mechanismen und Strukturen,
welche über reine Unifikation hinausgehen.
Beispiel 13.2.6 (F-Struktur von wiederholten Kategorien).
Wie kann man die Struktur von iterierten Kategorien auf der F-Struktur repräsentieren?
Der Operator F1 $ F2 (LFG: F1 ∈ F2) besagt: Die F-Struktur F1 ist Element in der mengenwertigen F-Struktur F2.
[ Weiter ] [ Zurück ] [ Zurück (Seitenende) ] [ Seitenbeginn ] [ Überkapitel ] [ Bitte Skript-Fehler melden ]