Reguläre Sprachen lassen sich durch FSA (endliche Automaten) beschreiben. Beim FSA handelt es sich um ein sehr einfaches Modell für informationsverarbeitende Maschinen ohne Speicher. Man kann sich dabei ein FSA als eine Maschine mit folgenden Komponenten vorstellen:

Ein Eingabeband, das in einzelne Felder unterteilt ist. Jedes dieser Felder kann mit einem Eingabezeichen (input alphabet) beschriftet sein, oder es kann leer sein.
Eine Kontrolleinheit, die unterschiedliche interne Zustände annehmen kann und die mit einem Lesekopf jeweils den Inhalt eines einzelnen Feldes des Eingabebandes lesen kann.

Graphisch sieht ein FSA somit folgendermassen aus (nach [Stu95], S.50) :

Formal wird ein FSA als Quintupel (S,I,S0,F,T) definiert , wobei

 S = endliche Menge von Zuständen (States)
 I = Eingabealphabet (input alphabet)
 S0= Startzustand (Initial state)
 F = Endzustand (final state), wobei F Teil der Menge S ist
 T = Zustandsübergangsfunktion (transition function): Zustand x Eingabe U {e} -> (neuer) Zustand  (U = vereinigt; {e} = Leerheitssymbol, Epsilon)

Im JFLAP werden die Zustände mit q0, ......qn bezeichnet.

Der FSA lässt sich mit Transitionsgraphen (transition graphs) und Zuständen graphisch als Zustandsdiagramm (transition graphs) darstellen. Beispiel:

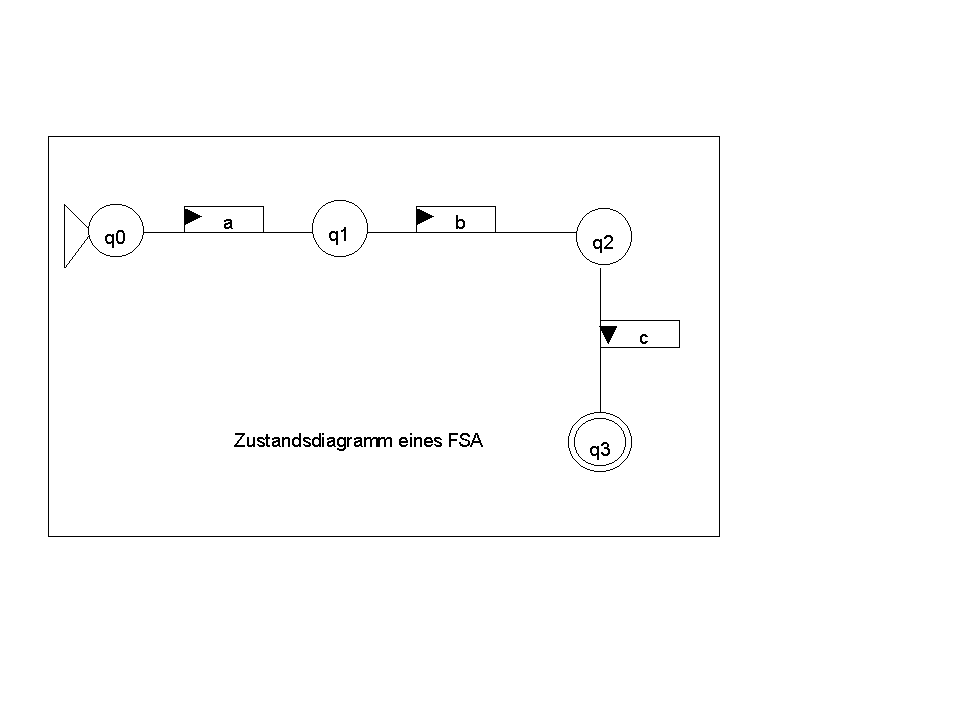
Die Zustandsübergangsfunktion T lautet für diesen Automaten:
(q0, a) -> q1
(q1, b) -> q2
(q2, c) -> q3

Dieser FSA entspricht folgender regulären Grammatik:
A -> a B
B -> b C
C -> c

Die Nichterminale bilden dabei die Zustände q<n>, die Terminalsymbole entsprechen den Übergangsfunktionen. Der Startzustand wird mit q0 bezeichnet.

Man unterscheidet zwischen deterministischem und nicht-deterministischem FSA (DFA, bzw. NFA genannt). Diese Unterscheidung ist auch als endlicher, bzw. nicht-endlicher FSA bekannt.