Für jeden Sprachtyp lassen sich eine Reihe von Entscheidungsproblemen angeben, die sich für den Sprachtyp lösen oder nicht lösen lassen. Eines der zentralen Probleme ist dabei das Erkennungsproblem (oder Wortproblem):

     Erkennungsproblem: Gehört eine Kette von Zeichen (ein Wort) einer Sprache ?

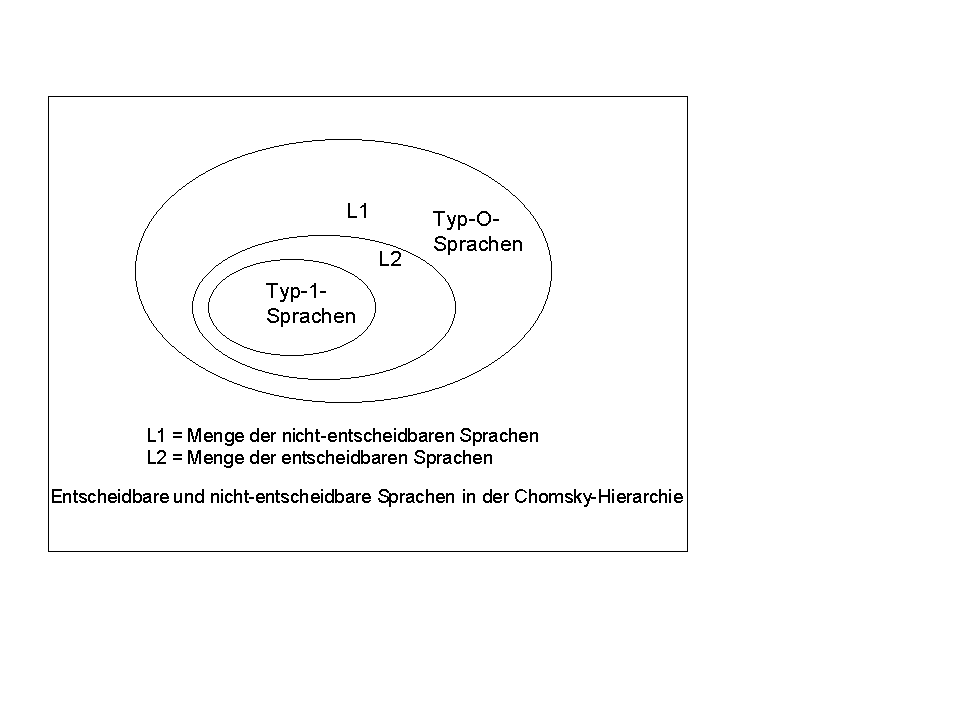
Man kann also keinen Algorithmus finden, der zu jedem vorgelegten Wort angibt, ob es einer Sprache zugehört oder nicht. Die Sprache ist in diesem Fall nicht-entscheidbar. Das Erkennungsproblem kann von der Turing Machine nicht gelöst, dh. nicht entschieden werden. Daraus ergibt sich das sog. "Halteproblem". Die Menge aller Sprachen (welche stets dem Sprachtyp 0 angehören) umfasst auch Sprachen, die nicht entscheidbar sind. Die Sprach-Hierarchie lässt sich somit auch folgendermassen darstellen (nach [Stu95], S.241):

Gesamtansicht des Diagramms (in einem separaten Fenster) hier.

Weitere Entscheidungsfragen befassen sich mit dem Leerheitsproblem, dem Aequivalenzproblem, dem Mehrdeutigkeitsproblem, etc. Die Beantwortung wird umso schwieriger, je allgemeiner die betrachtete Sprachklasse ist. Grundsätzlich lässt sich aber bei der Turing Machine keine dieser Fragen lösen. Eine ausführliche Behandlung zu dieser Problematik findest Du bei [Sud88], [Hop79] und [Kai72].