Introduction

Assignment #3 consists of 4 parts: The first part deals with decision trees, the second and the third part deal with probabilities, and the fourth part is about hidden markov models. Note that there is no programming part for this assignment. The total number of credits for this assignment is again 100 points.

Due date: Tue, May 17, 2011

Submitting your Solution

All material has to be submitted by e-mail to Lorenz Fischer by due date, 2 PM or be handed in in the lecture hall before the lecture starts. The subject of the email has to be PAI2011_A3.

Part 1: Decision Trees (30)

The goal of this exercise is to get familiarized with decision tree. Therefore a simple dataset about wether to go skiing or not is provided. The decision of going skiing depends on the attributes snow, weather, season, and physical condition as shown in the table below.

snow	weather	season	physical condition	go skiing
sticky	foggy	low	rested	no
fresh	sunny	low	injured	no
fresh	sunny	low	rested	yes
fresh	sunny	high	rested	yes
fresh	sunny	mid	rested	yes
frosted	windy	high	tired	no
sticky	sunny	low	rested	yes
frosted	foggy	mid	rested	no
fresh	windy	low	rested	yes
fresh	windy	low	rested	yes
fresh	foggy	low	rested	yes
fresh	foggy	low	rested	yes
sticky	sunny	mid	rested	yes
frosted	foggy	low	injured	no

a) Build the decision tree based on the data above by calculating the information gain for each possible node, as shown in the lecture. Please hand in the resulting tree including all calculation steps. (20)

Hint: There is a scientific calculator on calculator.com for the calculation of log2(x). By the way: log2(ax)=log10(ax)*log2(10) or log2(ax)=ln(ax)*log2(e).

b) Decide for the new instance given below whether to go skiing or not, based on the calculated classifiers: (5)

snow	weather	season	physical condition	go skiing
sticky	windy	high	tired	?

c) Now, an instance including missing values has to be classified (use the classifier built on the original data set): (5)

snow	weather	season	physical condition	go skiing
-	windy	mid	injured	?

Decide whether to go skiing or not.

Part 2: Bayesian Networks (20)

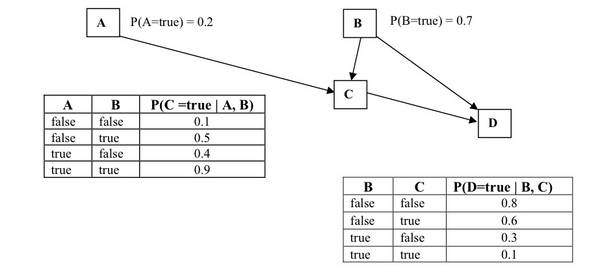
Consider the Bayesian Network below, where variables A-D are all Boolean-valued.

a) What is the probability that all four of these Boolean variables are false?

b) What is the probability that C is true, D is false, and B is true?

It is not sufficient to just put down the final result. Show your calculations!

Part 3: Probabilistic reasoning (20)

Imagine that 99% of the time RE Disease (RED) causes red eyes in those with the disease, at any point in time 2% of all people have red eyes, and at any point in time 1% of the population has RED.

You have red eyes. What is the probability you have RED?

Put down your complete calculations.

Part 4: Hidden Markov Models (30)

A professor wants to know if students are getting enough sleep. Each day, the professor observes whether the students sleep in class, and whether they have red eyes. The professor has the following domain theory:

The prior probability of getting enough sleep, with no observations, is 0.7.
The probability of getting enough sleep in night t is 0.8 given that the student got enough sleep the previous night, and 0.3 if not.
The probability of having red eyes is 0.2 if the student got enough sleep, and 0.7 if not.
The probability of sleeping in class is 0.1 if the student got enough sleep, and 0.3 if not.

What to do:

Formulate it as a hidden Markov model that has only a single observation variable.
Give the complete probability tables for the model.