Gewinnmaximierung

In der Einleitung haben Sie gelesen, dass ein Unternehmen seinen Gewinn maximieren möchte. Gewinn (Pi oder englisch Profit) entspricht dem Erlös (TR, englisch für Total Revenue) minus den Totalkosten (TC, englisch für Total Costs). Wir werden nun die Marksituation im vollkommenen Wettbewerb genauer betrachten. Vollkommener Wettbewerb bedeutet, dass alle Unternehmen ein homogenes (d.h. genau das gleiche) Gut verkaufen und exakt über alle Preise der Konkurrenten informiert sind, ebenso besitzen die Konsumenten vollkommene Information. Zudem sind die Unternehmen Mengenanpasser, d.h. der Preis ist fix und jedes Unternehmen passt seine produzierte Menge so an, dass der maximale Gewinn erwirtschaftet werden kann. Der vollkommene Wettbewerb ist ein theoretisches Modell und entspricht daher nicht unbedingt der Wirklichkeit, ermöglicht uns aber, komplexe Zusammenhänge in einer vereinfachten Umgebung genauer zu untersuchen. Ein Unternehmen kann somit den Gewinn steigern indem es entweder die Totalkosten senkt oder den Erlös steigert.

Der Erlös ist der Gegenwert, den ein Unternehmen für den Verkauf von bestimmten Gütern (oder Dienstleistungen) erhält. Der Erlös lässt sich relativ einfach als „verkaufte Menge * Verkaufspreis“ berechnen. Im Englischen wird der Erlös als Revenue bezeichnet.

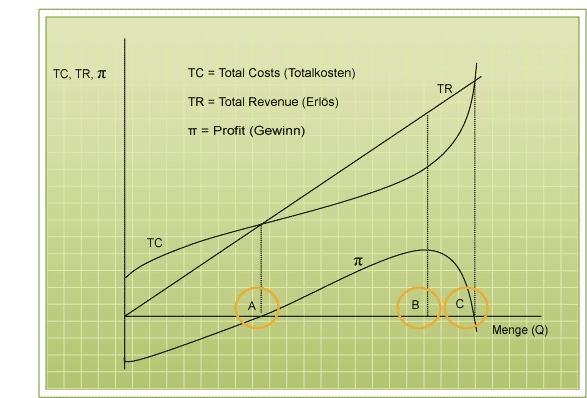Abbildung 12 - TC, TR und Gewinn

In der Abbildung 12 sehen wir, dass der Gewinn zunachst negativ ist, dies hangt damit zusammen, dass wenn nichts produziert wird, nur die fixen Kosten anfallen. Danach steigt der Gewinn stetig an. Sobald die Kosten (TC) gleich den Ertragen (TR) sind (Punkt A), geht der Gewinn (π) ins Positive. Der höchste Profit (das Gewinnmaximum) wird erreicht, wenn der Abstand der TR-Kurve und der TC-Kurve am grossten ist, sprich, wenn die Steigung der TR-Kurve gleich der Steigung der TC-Kurve ist (Punkt B). Sobald sich die TC und TR-Kurve ein zweites Mal schneiden (Punkt C) wird der Gewinn wieder negativ (G. Hildmann, 2005, S.111).

Wir wissen, dass die Steigung der totalen Kosten den marginalen Kosten (MC) entspricht. Wenn der Preis nun gleich den MC ist, ist der Gewinn maximal (Punkt B). Dieser Gedankengang ist sehr wichtig fur die weiteren Kapitel, daher hier nochmals in anderen Worten: Die Gesamterlose entsprechen dem, was ein Unternehmen an Gegenwert fur die verkauften Waren erhält, d.h. die verkaufte Menge multipliziert mit dem Verkaufspreis. Anhand der obigen Grafik sehen wir, dass im Profitmaximum (Gewinnmaximum) die Steigung der Ertrage gleich der Steigung der Kostenkurve sein muss. Da die Steigung der Geraden dem Preis entspricht, muss also auch die Steigung der Kosten im Gewinnmaximum dem Preis entsprechen.

Wir sehen, Ziel eines jeden Unternehmens muss die Menge Q sein, welche sich beim Gewinnmaximum, d.h. in Punkt B befindet. Wir werden die Gewinnkurve nun abschnittsweise genauer betrachten.

X-Achse Abb. 12: 0 – A
Die Kosten sind grösser als der Erlös, so dass ein Unternehmen einen Verlust macht. Der Grenzerlös, d.h. der Erlös, wenn eine zusätzliche Einheit produziert wird, ist höher als die zusätzlichen Kosten (Grenzkosten). Dies bedeutet, dass sich eine Steigerung der Produktion positiv auf den Profit auswirkt. Dies sehen wir auch anhand der Gewinnkurve, welche ansteigt.

X-Achse Abb. 12: A – B
Mittlerweile ist der Erlös grösser als die Kosten, es wird also ein Profit erwirtschaftet. Noch immer ist der Grenzerlös grösser als die Grenzkosten, daher lohnt es sich, die Produktion auszuweiten. Ob der Grenzerlös grösser oder kleiner als die Grenzkosten ist, sehen wir übrigens anhand der Steigungen. Von A nach B ist die Steigung der Erlöskurve (TR) immer grösser als die Steigung der Kostenkurve (TC). Somit steigt der Profit stetig an.

X-Achse Abb. 12: B – C
Von B nach C ist die Steigung der Kosten höher als die Steigung der Erträge, der Profit sinkt, es lohnt sich also nicht, die Produktion auszuweiten. In diesem Fall sollte das Unternehmen die Produktion reduzieren.

Der Gewinn kann auch mathematisch hergleitet werden. Der Gewinn π entspricht dem Erlös minus den Totalkosten.
π(Q) = TR(Q) - TC(Q)

max π(Q) = TR(Q) - TC(Q)
dπ / dQ = dTR / dQ - dTC / dQ --> dTR/dQ = MR und dTC/dQ = MC
dπ / dq = MR - MC
0 = MR - MC
MR = MC

Anmerkung: die TR entsprechen dem Preis mal der Menge, also P * Q. Nach Q abgeleitet ergibt dies dTR/dQ = P. Somit können wir anstelle von MR = MC auch P = MC schreiben (Ch. Ewerhart, 2007, S.280).