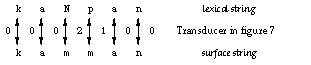In the Proceedings of the International Conference on Current Issues in Computational Linguistics. June 10-14, 1991. Universiti Sains Malaysia, Penang, Malaysia.

A later version of the paper appeared under the same title in The Last Phonological Rule, John Goldsmith, ed. University of Chicago Press. Chicago, Ill. 1993.

Some of the symbols did not survive the translation to HTML format, in particular, the Greek epsilon is throughout rendered as [epsilon], alpha as [alpha], and so on. The symbol [logicaland] in the phonetic transcription of "writer" represents an inverted v.

ORIGINAL SOURCE OF THIS ARTICLE: http://www.xrce.xerox.com/research/mltt/fst/articles/fsc-91/fsc91.html COPYRIGHT XRCE, XEROX

1. Introduction

This paper is a report on the application of finite-state methods to phonological and morphological analysis that has brought about spectacular progress in computational morphology over the last several years. We will review the fundamental theoretical work that underlies this progress and discuss its relevance for linguistics.

The two central problems in morphology are word formation and morphological alternations. The study of word formation is about the principles that govern the combinations of stems, affixes, and other types of morphemes. The problem of morphological alternations arises from the fact that a morpheme may have alternate realizations depending on its phonological environment and the composition of the word. Finite-state morphology is an attempt to account for these phenomena within the context of regular sets and regular relations. The claim that one of the problems can be solved in the finite-state state domain does not entail the same for the other, although the problems are certainly related. We concentrate here on morphological alternations, and put aside the question of word formation. We are primarily concerned with the type of rules used for describing morphological alternations and the principles of their application rather than the question of how morphemes should ideally be represented. The examples in this paper involve old-fashioned segmental representations but the main points apply equally well to feature-based and multi-tiered architectures.

There are two main strains of finite-state phonology: sequential and parallel. In sequential systems, surface forms are derived from underlying lexical forms by means of ordered rules through a series of intermediate representations. In a parallel description, rules constrain the realization of lexical forms directly without reference to intermediate stages. A parallel rule does not "apply" in the sense of changing one representation to another one, it is simply true or false of some pair of forms. Although it might be the case that one parallel rule takes precedence over another one it does not mean that their application is temporally ordered. Parallel descriptions are straight-forwardly declarative whereas seqential systems seem to have a more procedural flavor.

One important lesson that has been learned about the two styles of description is that in phonology they are formally equivalent. The difference between sequential and parallel approaches does not add to or subtract from the phenomena that can be described, although it may be important for other reasons. We start with this issue.

2. Origins of finite-state phonology

2.1 Johnson's discovery

The fundamental insight behind finite-state phonology is originally due to C. Douglas Johnson. In his 1972 book Formal Aspects of Phonological Description (based on the author's 1970 UC Berkeley dissertation) [1], Johnson demonstrated that phonological rules are much less powerful than the notation suggests. Although phonological rules are usually stated in the form of context-sensitive rewrite rules, as in (1), the generative power of phonological rules is drastically reduced by a simple constraint on their application.

(1)

[alpha] -> [beta] / [gamma] _ [delta]

Johnson observed that in derivations which involve repeated applications of the same rule, it is required that the domain of application moves to the left or to the right in the string. Phonological rewrite rules do not reapply to their own output within the same cycle. If rule (1) is used to derive [gamma]-[beta]-d, from [gamma]-a-d, any subsequent application of the rule on that cycle must leave [beta] unchanged thus affecting only [gamma] or d. Johnson demonstrated that the effect of the constraint is that the pairs of inputs and outputs produced by a phonological rule constitute a regular relation. A regular relation is a finite-state language in which the expressions are composed of symbol pairs rather than single symbols, a mapping of one regular set to another one. Simple finite-state languages (regular sets) are in one-to-one correspondence with ordinary finite-state automata; a regular relation corresponds to a finite-state transducer. What Johnson found out is that it only takes a finite-state machine, not a pushdown-store automaton or a Turing machine, to model a phonological rewrite rule.

To illustrate the effect of the constraint, consider the simple rule in (2).

(2)

[epsilon] -> ab / _ b (optional)

Rule (2) optionally inserts the string ab in front of b converting the string ab to aabb. Figure 1 illustrates what happens when the rule is reapplied n times. The italicized portion of the string is the newly inserted substring, the arrow marks the place of the next application. In column 1 the rule is being applied exclusively within the substring ab that results from the previous application in violation of the constraint; in column 2, the domain of application drifts to the right of the insertion site.

Figure 1: Two ways of applying [epsilon] -> ab / _ b

It is easy to see that the forbidden way of applying the rule in column 1 maps the input string ab to the strings in aaⁿbⁿb--a context-free language--whereas the conventional method of application in column 2 derives the regular language a[ab]ⁿb.

From the fact that the nested reapplications of the rule in column 1 give rise to a context-free language, we can deduce that in the general case, with no constraint on reapplication, the output language is also context-free. [1] Consequently, rule (2) describes a regular relation only if the rule is constrained not to apply within its own output.

A finite-state transducer is in other respects like an ordinary finite-state automaton except that it considers two strings rather than one. It can be conceived as a network consisting of states and labeled arcs. Final states are represented as double circles, non-final states by single circles. In a simple automaton, the arc labels are single symbols, in a transducer the labels are symbol pairs, x:y. In representing phonological rules, we follow the convention that the first member of the pair (the upper symbol), x, belongs to the input string, the second (lower) symbol, y, is part of the output string. If the members of the pair are identical, we simplify the notation by writing the pair as a single symbol. That is, in a transducer, the single label x means x:x.

A transducer implementing Rule (2) is shown in Figure 2.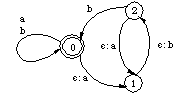

Figure 2. Transducer implementing [epsilon] -> ab / _ b

By convention, State 0 is the initial state. Here it is the only final state, States 1 and 2 are nonfinal. A special null symbol, [epsilon] ("epsilon"), allows the transducer to change states without moving its position on the string in question. For example, the [epsilon]:b arc in Figure 2 in linguistic terminology is a case of epenthesis, the output symbol b does not correspond to any symbol in the input.

Figure 3 traces the mapping of the string ab to aabb. The symbols on the upper side match the first member of an arc label, the symbols on the lower side match the corresponding second member of the pair; the numbers in the middle refer to states. Because the transducer doesn't block and ends up in a final state, Figure 3 demonstrates that the transducer allows ab to be realized as aabb.

Figure 3: Transducer mapping ab to aabb. (or vice versa)

Equivalently, we may just as well say that in Figure 3 the transducer is analyzing aabb as ab.

In modelling the application of the rule in a derivation, we start in State 0 with the symbols on the upper side and derive the output on the lower side by finding a path of arcs that matches the input and leads to a final state. In a case where the input and the output are identical, for example aba mapping to aba, we say that the rule has applied vacuously. The transducer in Figure 2 accepts any pair of strings that does not contain an epenthetic sequence terminating with [epsilon]:a [epsilon]:b which is not immediately followed by a b. That is the essential property that makes it an implementation of Rule 2.

2.2 Kaplan and Kay's rediscovery

Johnson's work seems to have received little notice at the time. In the early seventies it was widely accepted that finite-state and context-free grammars were in general not adequate for linguistics, especially not for syntax. In that context, it was perhaps uninteresting or implausible that phonological rule systems did not have the power that the notation seemed to imply. In any case, we don't know of any attempt to take advantage of this fact before it was independently rediscovered in a paper given at the 1981 LSA/ACL meeting in New York by Ronald M. Kaplan and Martin Kay, who had designed an algorithm for compiling rewrite rules to transducers.[2]

Kaplan and Kay made another important observation that Johnson also had noted in passing: regular relations are closed under serial composition. If we can model two rules applying in sequence by constructing a pair of transducers so that the output of the first transducer is the input side of the second one, we can also produce a single equivalent transducer by composition. The composed machine maps the input of the first transducer to the output of the second without generating any intermediate result. There is no corresponding composition operation for rewrite rules.

We illustrate this with two simple ordered rules (3a) and (3b). Here N stands for an underspecified nasal that is realized as a labial (N:m) or as a dental (N:n) depending on the environment.

				(3) (a)	N -> m / _ p; elsewhere, n.
				(b)	p -> m / m _

Applying in the order given, these rules convert the lexical string kaNpan to the surface string kamman, with kampan as an intermediate representation. Figures 4 and 5 show the individual transducers.[3]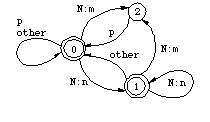

Figure 4: Transducer for N -> m / _ p

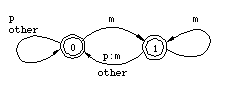Figure 5: Transducer for p -> m / m _

Figure 6 traces the derivation kaNpan ==> kampan ==> kamman as a transduction. As in Figure 3, the numbers refer to the states in the two transducers.

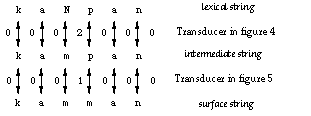Figure 6: Derivation as transduction

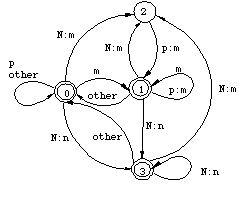
By examining the transitions in Figures 4 and 5, it is easy to see that the transducers correctly block any realization of an Np sequence that does not conform to the rules (3a) and (3b). For example, the transducer in Figure 4 requires a p after the pair N:m, thus kaNton cannot be realized as kamton.

The two-step derivation can be compressed to a single step by composing the two transducers. The basic idea in the composition algorithm for finite-state transducer is quite simple. Every state in the new machine corresponds to a pair of original states in the two transducers, starting with the two initial states. Every x:z arc in the new machine corresponds to an x:y arc in the upper transducer and an y:z arc in the lower transducer. The matching middle symbol y is eliminated.[4] The destination of the new arc is a state that corresponds to the destinations of the two original arcs. In general a composite transducer is larger than its components. In the worst case, the number of states in the composite machine is the product of the sizes of the original transducers.

Figure 7 presents the composite transducer derived from the two rules. It maps the lexical form kaNpan directly to kamman without an intermediate representation, as shown in Figure 8.

The transducer in Figure 7 encodes exactly the same lexical/surface relation as the sequence of the two original transducers. It allows the realization of N as m if and only if a p follows on the lexical side; it realizes p as m just in case an m precedes it--either an unchanging m or an m that comes from N, as required by the feeding order of the rules in (3). Although the constraint induced by this transducer is easily expressed in words, no corresponding rewrite rule exists because the realization of a lexical p as m is required and licensed by the output context, not by its environment on the input side. We will come back to this point shortly in the discussion of Koskenniemi's two-level formalism.

Because regular relations are closed under composition, any system of ordered phonological rules applying in sequence also describes a regular relation regardless of how many rules are involved. The intermediate stages in a phonological derivation can always be eliminated by composing a cascade of individual rule transducers into a single automaton that only recognizes two levels: a lexical level and a surface level. Figure 9 illustrates this possibility.

Figure 9: Replacing a cascade by a single transducer

From the point of view of phonological theory, the situation represented in Figure 9 means that, if the objective of a phonological description is to characterize the surface realization of lexical forms, the postulation of intermediate forms in a phonological derivation does not add to the descriptive power of the system. From a formal point of view, that mapping is a regular relation and it can be characterized in a purely declarative way by a single, but possibly very complex transducer. On the other hand, it can be argued that the individual rules in a cascade are linguistically and psychologically important because they make the complex relation comprehensible by decomposing it to a series of simple elementary relations. This indeed is the classical argument for some key features of generative phonology, in particular rule ordering [3]. However, as we shall see shortly, a similar decomposition can also be accomplished by unordered rules of a different sort.

For Kaplan and Kay the possibility of composing a single transducer from a cascade of transducers was not just an interesting theoretical result. They were looking for an efficient computational method for word recognition. In the service of that goal, converting rewrite rules to transducers is useful because transducers are bidirectional. Even more important is the possibility of composing them. A single transducer is far more efficient for recognition than an inverted cascade of individual rule transducers because of the inherent asymmetry of phonological rewrite rules. If rule (3b) is obligatory and the input string contains mp, then the next string on the way down towards the surface has mm in the place of mp. The converse does not hold. It does not follow from the rule that every occurrence of m in the context m _ comes from an underlying p. When used for analysis rather than generation, even obligatory rules become optional. From the lexical string kaNpan, the rules in (3) generate a single surface string, kamman, but the inverse mapping is one-to-many:

				(4) (a)	kaNpat ==> kammat
				(b)	{kammat, kaNpat, kampat} <== kammat

The amount of nondeterminism this introduces in recognition quickly multiplies in proportion to the number of rules involved. The uncertainty is not resolved until all the potential underlying strings are matched against the actual lexical forms. The advantage of a single transducer for recognition is that possible analyses do not multiply upwards; the upper side of the single transducer maps directly to the lexicon.

Although Kaplan and Kay solved the problem of converting individual phonological rules to transducers, the composition of large rule systems to a single transducer turned out to be unfeasible because of practical limitations. A single transducer encoding the complexities of a language like Finnish was too large for the computers available in the early 1980s.

2.3 Koskenniemi's two-level model

Kimmo Koskenniemi found another solution to this problem in his 1983 dissertation Two-level Morphology [4]. Knowing that the correspondence between lexical and surface forms is in any case a regular relation, he proposed a way of decomposing it to a set of rules that do not feed each other but work as parallel constraints.

In Koskenniemi's model, the surface realization of lexical forms is determined by a set of unordered constraints, each corresponding to a transducer. Every rule contains partial information about some aspect of the mapping; a surface form is a realization of a lexical form just in case all transducers accept the pair. The general architecture of the two-level model is illustrated in Figure 10.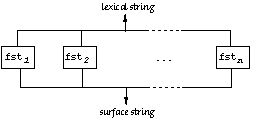

Figure 10: Transducers working in parallel

As the linking of the transducers in Figure 10 suggests, Koskenniemi's model presupposes that the transducers act in tandem. Every character pair is seen simultaneously by all the transducers, they all have to accept it at the same time.[5] Because of this linkage, it is possible to combine a set of Koskenniemi's machines to a single automaton by intersection, although in general intersection is not well-defined for finite-state transducers. But as far as the problem of recognition is concerned, there is no compelling practical need to combine the transducers to a single automaton. The two-level arrangement involves less nondeterminism than a cascade because all transducers relate surface strings directly to possible lexical strings. How many transducers there are in a parallel arrangement is for practical purposes insignificant in comparison to the effect that the depth of the cascade can have when rule transducers are linked vertically.

In an appendix to his dissertation, Koskenniemi presents 22 transducers that constitute a two-level description of morphological alternations in Finnish. These automata were painstakingly constructed by hand without rules. Many of them encode constraints that are not expressible as rewrite rules. As we already pointed out in discussing the transducer in Figure 7, it is not possible, for example, to write a single rule that makes the realization of lexical p as surface m depend on the surface environment of that m, although it is a simple matter to construct a transducer that implements the constraint.

The main theoretical contribution of Koskenniemi's thesis is a declarative rule formalism that is capable of expressing the constraints he had directly encoded as automata in the description of Finnish. The most salient feature of the formalism that distinguishes it from classical rewrite rules is that all context specifications can refer both to the lexical and to the surface context, hence the name two-level rule. Two-level rules are declarative; there is no derivation, no ordering. Another important aspect of the two-level formalism is that the rules are in effect modal statements about how a form can, must, or must not be realized. We will discuss the characteristics of this two-level formalism in the next section to set the state for a discussion of its expressive power vis-à-vis other types of rule systems.

3. Two-level rules

A simple two-level rule contains four pieces of information: a correspondence (cp) that the rule is about, an operator (op), a left context (lc) and a right context (rc); schematically: cp op lc _ rc. The correspondence part is typically a pair of characters x:y but it could in principle be a more complex expression. The upper symbol x is part of the lexical representation, the lower symbol y is part of the surface form, unless the symbol in question is the epsilon symbol. The context expressions are also two-level expressions.

3.1 Rule operators

The most fundamental aspect of the two-level rules is that they are deontic statements about correspondences that are possible, necessary, or prohibited in a certain environment. The modal force of the rule is expressed by the operator. The four operators proposed by Koskenniemi [4] are shown in table 1.

A left arrow (<=) rule is the closest analogue of an obligatory rewrite rule in classical generative phonology. Rules with the right arrow (=>) as the operator are similar to optional rewrite rules in that they allow but do not require some correspondence in the given environment. However, these comparisons are not exact because standard rewrite rules can only refer to the upper part of the two-level context. In practice, the most useful rule operator seems to be <=>, which combines the effect of <= and =>. Constraints that pertain only to one side of the lexical/surface relation can be written using a correspondence expression that leaves the other side unspecified. For example, a: /<= c _ d is a constraint on lexical forms.

3.2 Two-level contexts

Let us first consider a simple example we are already familiar with: the realizations of N and p in Figures 4, 5, and 7. Figure 11 illustrates what we would like our rules to say.

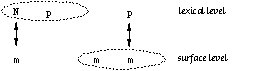
Figure 11: Lexical vs. surface context

				(5) (a)	N:m <=>    _ p:
				(b)	p:m <=> :m _

The location of the colon in p: indicates the p in (5a) is a lexical symbol--with some surface realization that is not relevant for (5a). Because it only refers to the lexical context, (5a) is for all practical purposes equivalent to the rewrite rule in (3a). In (5b), the colon to the left of m in :m in indicates that m is a surface symbol here. This makes (5b) different from the rewrite rule in (3b). Because (5a) and (5b) are independent from each other, they can apply simultaneously whereas the application of (3a) and (3b) must be ordered.

The transducers for the two-level rules in (5) correspond very closely to the automata we have already seen Figures 4 and 5. In fact the transducers for (3a) and (5a), shown in Figure 4, are identical. The transducer for (5b), in Figure 12, is in a subtle way different from Figure 5. The difference is in the arcs leading to and from State 1, which controls the realization of p as m. In Figure 12, we reach that state by encountering a surface m which can be a realization of either m or N on the lexical side. Figure 5 only allows the former possibility. Another difference, not relevant here, is that the p:m arc loops back to State 1 instead of going back to the initial state. It means that the realization of p as m would spread to the right over a sequence of adjacent p's.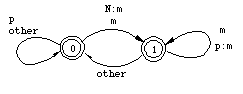

Figure 12: Transducer for p:m <=> :m _

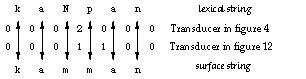Figure 13: Transduction with parallel transducers

The two transducers in 13 are operating in tandem; if either one of them would block or end up in a non-final state, the mapping between kaNpan and kamman would fail. For example, the realization of kaNpan as kampan fails at the point shown in Figure 14 because in the transducer for (5b), there is no transition for p in State 1 (p is not included in other since it is explicitly mentioned on another arc in the same machine).

Figure 14: Non-allowed correspondence

It is important to realize that two-level rules always refer to both the lexical and the surface contexts, either implicitly or explicitly. Changing (5a) to

(5) (a')

N:m <=> _ p

would change its meaning. The right-hand context of (5a') is "lexical p realized as p on the surface." For the case at hand, (5a') is wrong because it does not allow the kaNpan to be realized as kamman.

3.3 Advanced features

The context specification of a two-level rule may be more complicated than the simple examples we have been considering, it can be any regular expression. A rule compiler for the formalism developed by Karttunen, Koskenniemi, and Kaplan [5] allows the construction of complex regular expression with the operators listed in table 2.

As the use of C and V in Table 2 suggests, context specifications may include other symbols besides character pairs assuming that they are defined by some regular expression. If a set of symbols behave alike with respect to several rules, it may be useful to define them as a set. In part this facility makes up for the lack of distinctive features in current implementations of the two-level formalism.

Two other important enhancements are rules with multiple contexts and rules with variables. Examples are given in (6) and (7).

				(6)	b:p <=> #: _
					_ #:

Rule 6 says that initial and final b's are devoiced to p. For the => operator, multiple contexts have a disjunctive effect: b can be realized as p, if it is located either after or before a word boundary. For the <= operator, multiple contexts are equivalent to a conjunction: lexical b must be realized as p initially and finally.

Variables in the two-level formalism are analogous to a-valued features in generative phonology. Rule 7 inserts a copy of the preceding vowel in an hn cluster.

(7)

[epsilon]:Vx <=> Vx h _ n ; where Vx in V

For example, it maps lahna to lahana and vice versa.

These and other similar enhancements to the basic two-level formalism have no effect on the formal power of the system; they just make it more convenient to express constraints that are typical in the phonology and orthography of many languages.

With the help of the rule compiler [5] that converts two-level rules to transducers, comprehensive rule systems have been developed for a number of languages. These include English (Lauri Karttunen), Finnish (Kimmo Koskenniemi), Russian (Liisa Vilkki), and French (Carol Neidle, Annie Zaenen) all unpublished so far.[6] Kenneth Beesley [5] has developed an extensive two-level analysis of Arabic [6].

4. Discussion: sequential vs. parallel descriptions

So far we have discussed two strains of finite-state phonology: the original Johnson, Kaplan, Kay cascade that models sequential rewrite rules and Koskenniemi's parallel formalism that was inspired by the realization that systems of the first kind describe regular relations. The details of the mapping from lexical to surface forms in some language can be very complex but we can be sure that there are at least two ways of decomposing that relationship into a set of more primitive relations. Although we have no algorithm that would convert a cascade of rewrite rules to an equivalent, and equally elegant, set of two-level rules, or vice versa, there is no substantive difference with respect to the complexity of phenomena that can be described. From a computational point of view, the two-level model has a practical advantage for reasons discussed in section 2 but that does not answer the question which style is better for linguistic description. In the absence of persuasive psychological evidence for sequential or parallel application of phonological principles to settle the issue, we can still ask whether the phenomena that are common in natural languages are easier to describe in one formalism rather than the other.

The crux of the matter is the question about the role that intermediate representations play in generative phonology. What is the insight about language that is captured by the ordered application of rewrite rules? There is an enormous body of literature on this topic ranging from the 1930s to a recent article by Bromberger and Halle [7] that reiterates the classical arguments of Chomsky and Halle [3]. The problem with all of the standard references is that the arguments are valid only against competing descriptions that are similar in every other respect except for not having ordered rules. They have no force with respect to rules that are of a different sort, such as the two-level constraints in a Koskenniemi-style system. We consider three such cases here. More examples of the same type can be found in Lakoff [8].[7]

4.1 Simple extrinsic order

Perhaps the best known single example in favor of rule ordering [3, 7] is the contrast between the words writer [r[logicaland]yDer] and rider [rayDer] in Canadian English. This involves the raising of ay to [logicaland]y in front of a voiceless element and the merger of t and d to a voiceless flap D. The standard account for the lack of [logicaland]y in rider is that the raising rule is applied before d becomes voiceless. Simplifying somewhat, the key idea is that Rule (8a) precedes Rule (8b).

				(8) (a)	ay -> [logicaland]y / _ -V
				(b)	t,d -> D / V _ V

Here -V stands for the feature [- voiced], V for vowels.

Another, equally simple way of describing the contrast is to say that the ay:[logicaland]y correspondence is controlled by the lexical environment alone. The unordered two-level rules in (9) are equivalent to the sequence of ordered rules in (8).

				(9) (a)	ay:[logicaland]y <= _ -V:
				(b)	t:D | d:D <= V _ V [8]

The composition of the two transducers implementing (8a) and (8b) is the same as the intersection of the automata corresponding to (9).

In addition to being equivalent with respect to the writer~rider contrast, (8) and (9) can both be modified in a simple way to describe Canadian dialects in which writer and rider are pronounced the same way: [r[logicaland]yDer]. In the case of (8), the order of application is reversed, in the case of (9), the context part of (9a) is replaced by _ :-V to indicate that the ay:[logicaland]y correspondence is required when the following surface element is voiceless.

This case is typical of the many textbook examples that explain why rules must be ordered. It rests on the implicit assumption that any adequate formal description of the phenomenon by necessity involves a sequence of structure changing operations that are constrained only by the representation to which they apply. It overlooks the possibility that the very same input/output relation can also be characterized by constraints not limited in that way.

4.2 Disjunctive order

Another common type of example of rule ordering involves a pair of rules that pertain to the same element and the environment of one rule subsumes the environment of the other. For example, in Finnish consonant gradation, intervocalic k generally disappears in the weak grade. However, between two high labial vowels k is realized as v. Consequently, the genitive of maku `taste' is maun but the genitive of puku `dress' is puvun.

The problem with the description just stated is that the k in -uku- is also an instance of an intervocalic k. The rules contradict each other.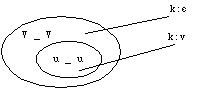

Figure 15: A case of subsumption

This situation is not a problem for the derivational phonologist because the rule that turns k to v in the more specific context can be ordered before the deletion rule that applies in the more general environment. This is known as disjunctive ordering. A rule with a more specific environment has precedence over a general rule if the two rules are in conflict. Because this is a very common state of affairs, disjunctive ordering is considered a part of the phonological theory, even though exceptions are allowed.

In the two-level framework, there seemingly is a problem. If the rules are formulated as in (10), they do not work as intended.[9]

				(10) (a)	k:v <=> u _ u C [#: | C]
				(b)	k:[epsilon] <= V _ V C [#: | C]

Without ordering, the rules in (10) are in a fatal conflict with one another. According to (10a), the genitive of puku `dress' should be puvun, (10b) says it must be puun. The result of the contradiction is that puku cannot be realized in the genitive at all.

There is of course a simple, but undesirable, fix. One could make the general rule a bit more specific by subtracting from it the context of the more specific rule:

				(10) (b')	k:[epsilon] <=	[V - u]	_	[V - u] C [#: | C]
						[V - u]	_	u C [#: | C]
						u	_	[V - u] C [#: | C]

This solves the technical difficulty but it provides an argument for the derivational phonologist. (10b') is clearly more complicated than the original version.[10] The rule has lost its generality. The simpler formulation in (10b) can be maintained only by imposing an order on the rules, either by stipulation or by a general principle.

There is another parallel solution that is not open to the same objection. We can avoid the conflict just as easily by rephrasing (10b) as (11b).

				(11) (a)	k:v <=> u _ u C [#: | C]
				(b)	k:[epsilon] | k:v <= V _ V C [#: | C]

There is only one difference between (10) and (11). (11b) says that in the gradation context k must either be deleted or realized as v. Unlike (10b'), which is clearly a complication of the original version, (11b) is actually simpler than (10b). It is less informative than the rule it replaces because the relation expressed by (10b) is--in the literal sense--a subset of the relation expressed by (11b).[11] So the change from (10) to (11) is not a complication but a simplification.[12] Note that the general rule now depends on the specific one to produce the right outcome. In the case of maku `taste', (11b) allows the genitive to be either maun or mavun. But the latter possibility is not permitted by (11a) leaving only the correct form maun.

The simplest descriptive solution to the problem posed by conflicts like (10) is to make the general rule more general.[13] In context of Koskenniemi's two-level formalism, this is an obvious move. It takes advantage of underspecification, a very useful option in a declarative system of constraints. It is not the responsibility of any single rule to get everything right because other rules will also have their say.

4.3 Free ride

Underspecification is also a natural solution for overlapping harmony systems such as is found in Turkish. Turkish suffixes contain two types of harmonizing vowels. One is a low vowel, represented here as E, that is realized either as a or e depending on the backness of the preceding vowel. The other is a high vowel, I, that assimilates to the preceding vowel both in backness and in roundness, thus it has four contextually determined realizations i, i, u, and ü. To encode the basic harmony facts as two-level constraints it is convenient first to define a few auxiliary terms to make up for the lack of a more sophisticated representation.

				(12)	RndVowel = o u ö ü
					BackVowel = a i o u
					HighVowel = i i u ü
					HiRndVowel = u ü
					HiBackVowel = i u
					LowBackVowel = a
					HiHrmVowel = I [epsilon]
					LowHrmVowel = E

We give the epsilon symbol the same status as the high harmonizing vowel I for reasons that will become clear in a moment. With the help of these somewhat cumbersome definitions, the two harmony rules themselves become easier to state.

				(13)	Rounding Harmony
					HiHrmVowel:HiRndVowel <=> :RndVowel :C* _

				(14)	Back Harmony
					Vx:Vy <=> :BackVowel :C* _ ;
					where Vx in (HiHrmVowel LowHrmVowel)
					Vy in (HiBackVowel LowBackVowel) matched [14]

In this case, the corresponding transducers look simpler than the rules themselves. They are both just two-state automata. In the initial state no harmonic vowel has been seen; the second state is the situation after a surface round vowel (13) or a surface back vowel (14) has been encountered. In the initial state the harmonizing vowel has its default realization, unrounded for I, front vowel for E. In State 1 the established harmony spreads.

Figure 16: Rounding Harmony

Figure 17: Back Harmony

It is easy to see in Figures 16 and 17 that neither transducer completely specifies the quality of the harmonizing vowel. The rounding harmony rule allows and requires I to be realized as u or ü after a rounded vowel but does not specify which one; the back harmony rule allows and requires I to be realized as u or i after a back vowel without completely determining the outcome either. But taken together the two rules cover all the cases completely and correctly. For example, the Genitive case of mektub `letter', lexically represented as mektubI, is realized as mektubu because the I:u correspondence is the only realization of I that satisfies both constraints in this word.

Getting the harmony right for lexically specified harmonizing vowels is only a part of the problem. In Turkish certain consonant clusters are broken by an epenthetic vowel that is subject to the same harmony rules as the lexically specified I. For example, the stem of isim `name' may be lexically specified as ism because the sm cluster shows up in all forms of the paradigm, such as the Objective form ismi, where it is not syllable final. Similarly for ogul~oglu. [15]

In system of ordered rules, the behavior of the epenthetic vowel with respect to harmony is no problem. Without going into details about what the relevant consonant clusters are, we can specify the epenthesis rule simply as (15),

(15)

[epsilon] -> I / Cx _ Cy

where Cx and Cy constitute a cluster of the relevant type. If the epenthesis rule is ordered before the vowel harmony, the inserted vowel gets a "free ride" on the rules that pertain to lexically specified I's. The epenthesis rule does not have to duplicate the effect of the harmony rules. Another apparent point in favor of rule ordering.

But it turns out that a virtually identical analysis can also be stated in terms of unordered constraints. In fact, we he have already done that by grouping I and [epsilon] together in the definition of HiHrmVowel in (12). Figures 16 and 17 show that, in addition to specifying the correct realization of the two harmonizing vowels I and E, the rules (13) and (14) also select the appropriate epenthetic pair, [epsilon]:i, [epsilon]:i, [epsilon]:u, or [epsilon]:ü, for each type of surface environment. A two-level version of the epenthesis rule, (16), has the intended effect without any ordering statements.

(16)

[epsilon]:HighVowel <=> Cx _ Cy

In fact, (16) itself is simpler than (15) because it contains less information.[16]

5. Conclusion

In the preceding discussion we have examined three examples that are typical of the kind arguments that have been advanced in order to demonstrate that the best way to characterize the mapping between lexical and surface forms is in terms of ordered rules. In the cases we have studied, the argument clearly fails; we think there are no better ones around.[17] The fundamental problem with such arguments is that they only look for alternative solutions in the space of rewrite rules, that is, rules that constrain the realization of some element only in terms of its neighbors on the input side. If one has been raised as a generative linguist, like most of us have been, it is difficult to see that such rules have no privileged status. One important lesson that can be learned from the exercise of converting rewrite rules to transducers is that there are simple constraints on regular relations that rewrite rules cannot capture. That is one of the insights in Koskenniemi's rule formalism and Lakoff's recent work [8] on `cognitive phonology.'[18]

Although it is a fact that phonological rule systems in many cases can be reduced to a two-level system without any loss of descriptive adequacy, there is no need to insist on a two-level description. There are good reasons to think, for example, that the intercalating morphology of Semitic languages is most naturally described in a three or four-level system [9]. More than two levels are also needed for the formalization of multitiered or multiplanar representations [10]. It is not known whether all the phenomena described by means of such representations can be reduced to regular n-level relations in the same way as classical rewrite systems reduce to two-level relations but it looks like a good conjecture that most of them are of that type.[19] If that is the case, rules that simultaneously constrain elements on more than two planes or tiers can be implemented by a simple generalization of two-level transducers to finite-state automata with n-tuple labels.

The demonstration that classical phonology deals with regular relations has two important benefits. On one hand, it has given us a semantics for the rule formalism itself. We have precise answers to questions such as "Are these descriptions equivalent?" "Is this rule more general than that one?" Secondly, because the mathematical properties of the formalism are known, we have the means to compile linguistic descriptions to efficiently functioning programs for recognition and generation regardless of the complexity of the description. In this respect, it is true that "phonology is different" from other areas of linguistics, although that is not quite what Bromberger and Halle [7] had in mind.

References

[1] Johnson, C. Douglas. Formal Aspects of Phonological Description. Mouton. The Hague. 1972.

[2] Kaplan, Ronald M. and Martin Kay. Phonological rules and finite-state transducers [Abstract]. Linguistic Society of America Meeting Handbook. Fifty-sixth Annual Meeting, December 27-30, 1981. New York.

[3] Chomsky, N. and M. Halle. The Sound Pattern of English. Harper and Row. New York. 1968.

[4] Koskenniemi, Kimmo. Two-level Morphology. A General Computational Model for Word-Form Recognition and Production. Department of General Linguistics. University of Helsinki. 1983.

[5] Karttunen, Lauri, Kimmo Koskenniemi, and Ronald M. Kaplan. A Compiler for Two-level Phonological Rules. In Dalrymple, M. et al. Tools for Morphological Analysis. Center for the Study of Language and Information. Stanford University. Palo Alto. 1987.

[6] Beesley, Kenneth R. Finite-State Description of Arabic Morphology. The Proceedings of the Second Cambridge Conference: Bilingual Computing in Arabic and English. Sept. 5-7, 1990. Cambridge.

[7] Bromberger, Sylvain and Morris Halle. Why Phonology is Different. Linguistic Inquiry 20: 51-70. 1989.

[8] Lakoff, George. Cognitive Phonology. Presented at the Berkeley Conference on Nonderivational Phonology. May 26, 1989.

[9] Kay, Martin. Nonconcatenative Finite-State Morphology. Proceedings of the 3rd Conference of the European Chapter of the Association for Computational Linguistics. Copenhagen. 1987.

[10] Goldsmith, John J. Autosegmental and Metrical Phonology. Blackwell. London, 1990.

[11] Kornai, András. Formal Phonology. Doctoral Dissertation. Stanford University. Stanford, 1991.

Footnotes

[1] This follows from the fact that the intersection of the output language L with the regular language a*b* leaves aⁿbⁿ. Because aⁿbⁿ is not regular, neither is L.

[2] Only an abstract of the paper in the Meeting Handbook [2] has been published. [NOTE: This is no longer true. Kaplan and Kay 1994 descends from their 1981 LSA presentation. L.K.]

[3] The label other stands for all symbols in the alphabet that are not explicitly shown.

[4] This applies only when y != [epsilon]. The treatment of x:[epsilon] and [epsilon]:z cases is a bit more complicated.

[5] One important consequence of this requirement is that epsilon transitions become synchronized. No transducer can make a move on one string while keeping the other one in place unless all the other transducers do the same. Without this constraint there is no guarantee that the relations described by the individual transducers add up to a regular relation when considered as a whole.

In general, the intersection of two regular relations is not regular. For example, let R1 be the relation <xⁿ:aⁿb*>, and R2 the relation <xⁿ:a*bⁿ>. R1 corresponds to a finite-state transducer that maps any number of x's to the same number of a's followed by any number of trailing b's, R2 matches the number of x's and b's allowing any number of preceding a's. The intersection R1[intersection]R2, <xⁿ:aⁿbⁿ>, cannot be generated by a finite-state automaton because it maps a regular set to a context-free language.

In Koskenniemi's system the two transducers for R1 and R2 have to agree on the location of epsilons because they are running in tandem. Consequently, acting together they just map xⁿ to the empty set. That relation is of course regular.

[6] They were developed in the course of constructing spelling checkers and morphological analyzers for these languages.

[7] The formalism in Lakoff's paper is different from ours but the conclusions are strikingly similar. The constraints are expressed in a semi-formal style as graphs (similar to Figure 11) that can easily be translated to our notation. Lakoff recognizes three rather than two levels but equally simple two-level analyses can be constructed for all of his examples. A reduction from three to two levels could also be accomplished by simple composition because no constraint refers to all three levels at once.

[8] The vertical bar in t:D | d:D means disjunction. (9a) means "If t or d occurs between vowels it must be realized as D."

[9] The symbol # stands for word boundary. The context specification V _ V C [#: | C] is a rather clumsy way of expressing the idea that consonant gradation involves closed syllables. It will have to suffice here. The actual conditions for consonant gradation in Finnish are in any case more complicated. The operator in (10a) is <=> because the k:v realization is specific to this environment, <= in (10b) indicates that there are other environments in which k is deleted in Finnish.

[10] Three contexts are needed in (10b') to cover all the environments. The first context requires the deletion of k in cases like sika:sian 'pig', the second is for words like maku:maun 'taste', the third for suka:suan 'comb'. Only k's that are flanked by u's on both sides, puku:puvun 'dress', are exempt from the rule.

[11] This fact can be shown most easily by compiling the rules to transducers because we can quickly determine whether a language accepted by one finite-state automaton subsumes the language of another machine even if the languages in question are infinite. By that test, (11b) does indeed subsume (10b) but not vice versa.

[12] By the same argument, p | q is simpler than p; p is simpler than p [logicaland] q. The less information a proposition contains, the more situations there are in which it is true.

[13] The two-level rule compiler actually locates and resolves problems of this type automatically. In particular, it will compile the rules in (10) as (11), unless the user turns off the option. This is useful for more complicated rules in which a conflict arises under a certain assignment of a value to a variable but not in other cases. With the compiler taking care of the special case, the general rule can be stated more concisely.

[14] Here "matched" means that the assignment of values to the variables Vx and Vy is synchronized so that when Vx has its n^th value Vy is also bound to its n^th value. See [5] for details.

[15] For the sake of the argument, let us ignore the alternative analysis that the contrast is due to deletion rather than epenthesis.

[16] The correspondence part of (15) is equivalent to a disjunction: [epsilon]:i | [epsilon]:i | [epsilon]:u | [epsilon]:ü.

[17] We have not mentioned the issue of cyclic ordering because it very much depends on assumptions about word formation that we cannot go into here. Let us simply state that, in our opinion, the arguments for cyclic ordering are weaker than the ones that we discuss.

[18] It is not clear whether Lakoff himself realizes that the system he describes is yet another version of finite-state phonology. The paper does not address this issue.

[19] See Ch. 2 of Kornai [11] for a demonstration that autosegmental rules express finite-state constraints.